As someone who heads a hydrogen energy company, REB Research, I regularly have to tip toe about nuclear power, a rather large elephant among the clean energy options. While hydrogen energy looks better than battery energy in terms of cost and energy density, neither are really energy sources; they are ways to transport energy or store it. Among non-fossil sources (sources where you don’t pollute the air massively) there is solar and wind: basically non-reliable, low density, high cost and quite polluting when you include the damage done making the devices.
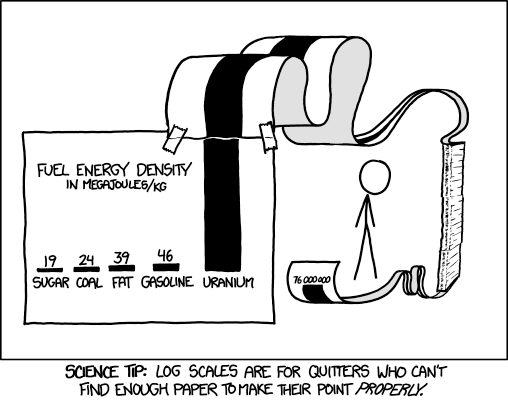
Compared to these, I’m happy to report that the methanol used to make hydrogen in our membrane reactors can come from trees (anti-polluting), even tree farming isn’t all that energy dense. And then there’s uranium: plentiful, cheap and incredibly energy dense. I try to ignore how energy dense uranium is, but the cartoon below shows how hard that is to do sometimes. Nuclear power is reliable too, and energy dense; a small plant will produce between 500 and 1000 MW of power; your home uses perhaps 2 kW. You need logarithmic graph paper just to compare nuclear power to most anything else (including hydrogen):
A tiny amount of uranium-oxide, the size of a pencil will provide as much power as hundreds of train cars full of coal. After transportation, the coal sells for about $80/ton; the sells for about $25/lb: far cheaper than the train loads of coal (there are 100-110 tons of coal to a train-car load). What’s more, while essentially all of the coal in a train car ends up in the air after it’s burnt, the waste uranium generally does not go into the air we breathe. The coal fumes are toxic, containing carcinogens, carbon monoxide, mercury, vanadium and arsenic; they are often radioactive too. All this is avoided with nuclear power unless there is a bad accident, and bad accidents are far rarer with nuclear power than, for example, with natural gas. Since Germany started shutting nuclear plants and replacing them with coal, it appears they are making all of Europe sicker).
It is true that the cost to build a nuclear plant is higher than to build a coal or gas plant, but it does not have to be: it wasn’t that way in the early days of nuclear power, nor is this true of military reactors that power our (USA) submarines and major warships. Commercial nuclear reactors cost a lot largely because of the time-cost for neighborhood approval (and they don’t always get approval). Batteries used for battery power get no safety review generally though there were two battery explosions on the Dreamliner alone, and natural gas has been known to level towns. Nuclear reactors can blow up too, as Chernobyl showed (and to a lesser extent Fukushima), but almost any design is better than Chernobyl.
The biggest worry people have with nuclear, and the biggest objection it seems to me, is escaped radiation. In a future post, I plan to go into the reality of the risk in more detail, but the worry is far worse than the reality, or far worse than the reality of other dangers (we all die of something eventually). The predicted death rate from the three-mile island accident is basically nil; Fukushima has provided little health damage (not that it’s a big comfort). Further, bizarre as this seems the thyroid cancer rate in Belarus in the wind-path of the Chernobyl plant is actually slightly lower than in the US (7 per 100,000 in Belarus compared to over 9 per 100,000 in the USA). This is clearly a statistical fluke; it’s caused, I believe, by the tendency for Russians to die of other things before they can get thyroid cancer, but it suggests that the health risks of even the worst nuclear accidents are not as bad as you might think. (BTW, Our company makes hydrogen extractors that make accidents less likely)
The biggest real radiation worry (in my opinion) is where to put the waste. Ever since President Carter closed off the option of reprocessing used fuel for re-use there has been no way to permanently get rid of waste. Further, ever since President Obama closed the Yucca Mountain burial repository there have been no satisfactory place to put the radioactive waste. Having waste sitting around above ground all over the US is a really bad option because the stuff is quite toxic. Just as the energy content of nuclear fuel is higher than most fuels, the energy content of the waste is higher. Burying it deep below a mountain in an area were no-one is likely to live seems like a good solution: sort of like putting the uranium back where it came from. And reprocessing for re-use seems like an even better solution since this gets rid of the waste permanently.
I should mention that nuclear power-derived electricity is a wonderful way to generate electricity or hydrogen for clean transportation. Further, the heat of hot springs comes from nuclear power. The healing waters that people flock to for their health is laced with isotopes (and it’s still healthy). For now, though I’ll stay in the hydrogen generator business and will ignore the clean elephant in the room. Fortunately there’s hardly any elephant poop, only lots and lots of coal and solar poop.