Category Archives: Science: Physics, Astronomy, etc.

In praise of openable windows and leaky construction

Leave a reply

It’s summer in Detroit, and in all the tall buildings the air conditioners are humming. They have to run at near-full power even on evenings and weekends when the buildings are near empty, and on cool days. This would seem to waste a lot of power and it does, but it’s needed for ventilation. Tall buildings are made air-tight with windows that don’t open — without the AC, there’s be no heat leaving at all, no way for air to get in, and no way for smells to get out.

The windows don’t open because of the conceit of modern architecture; air tight building are believed to be good design because they have improved air-conditioner efficiency when the buildings are full, and use less heat when the outside world is very cold. That’s, perhaps 10% of the year. 

No openable windows, but someone figured you should suffer for art

Modern architecture with no openable windows. Someone wants you to suffer for his/her art.

Another reason closed buildings are popular is that they reduce the owners’ liability in terms of things flying in or falling out. Owners don’t rain coming in, or rocks (or people) falling out. Not that windows can’t be made with small openings that angle to avoid these problems, but that’s work and money and architects like to spend time and money only on fancy facades that look nice (and are often impractical). Besides, open windows can ruin the cool lines of their modern designs, and there’s nothing worse, to them, than a building that looks uncool despite the energy cost or the suffering of the inmates of their art.

Most workers find sealed buildings claustrophobic, musty, and isolating. That pain leads to lost productivity: Fast Company reported that natural ventilation can increase productivity by up to 11 percent. But, as with leading clothes stylists, leading building designers prefer uncomfortable and uneconomic to uncool. If people in the building can’t smell an ocean breeze, or can’t vent their area in a fire (or following a burnt burrito), that’s a small price to pay for art. Art is absurd, and it’s OK with the architect if fire fumes have to circulate through the entire building before they’re slowly vented. Smells add character, and the architect is gone before the stench gets really bad. 

No one dreams of working in an unventilated glass box.

No one dreams of working in a glass box. If it’s got to be an office, give some ventilation.

So what’s to be done? One can demand openable windows and hope the architect begrudgingly obliges. Some of the newest buildings have gone this route. A simpler, engineering option is to go for leaky construction — cracks in the masonry, windows that don’t quite seal. I’ve maintained and enlarged the gap under the doors of my laboratory buildings to increase air leakage; I like to have passive venting for toxic or flammable vapors. I’m happy to not worry about air circulation failing at the worst moment, and I’m happy to not have to ventilate at night when few people are here. To save some money, I increase the temperature range at night and weekends so that the buildings is allowed to get as hot as 82°F before the AC goes on, or as cold as 55°F without the heat. Folks who show up on weekends may need a sweater, but normally no one is here. 

A bit of air leakage and a few openable windows won’t mess up the air-conditioning control because most heat loss is through the walls and black body radiation. And what you lose in heat infiltration you gain by being able to turn off the AC circulation system when you know there are few people in the building (It helps to have a key-entry system to tell you how many people are there) and the productivity advantage of occasional outdoor smells coming in, or nasty indoor smells going out.

One irrational fear of openable windows is that some people will not close the windows in the summer or in the dead of winter. But people are quite happy in the older skyscrapers (like the empire state building) built before universal AC. Most people are nice — or most people you’d want to employ are. They will respond to others feelings to keep everyone comfortable. If necessary a boss or building manager may enforce this, or may have to move a particularly crusty miscreant from the window. But most people are nice, and even a degree of discomfort is worth the boost to your psyche when someone in management trusts you to control something of the building environment.

Robert E. Buxbaum, July 18, 2014. Curtains are a plus too — far better than self-darkening glass. They save energy, and let you think that management trusts you to have power over your environment. And that’s nice.

Dr. Who’s Quantum reality viewed as diffusion

3 Replies

It’s very hard to get the meaning of life from science because reality is very strange, Further, science is mathematical, and the math relations for reality can be re-arranged. One arrangement of the terms will suggest a version of causality, while another will suggest a different causality. As Dr. Who points out, in non-linear, non-objective terms, there’s no causality, but rather a wibbly-wobbely ball of timey-wimey stuff.

Time as a ball of wibblely wobbly timey wimey stuff.

Reality is a ball of  timey wimpy stuff, Dr. Who.

To this end, I’ll provide my favorite way of looking at the timey-wimey way of the world by rearranging the equations of quantum mechanics into a sort of diffusion. It’s not the diffusion of something you’re quite familiar with, but rather a timey-wimey wave-stuff referred to as Ψ. It’s part real and part imaginary, and the only relationship between ψ and life is that the chance of finding something somewhere is proportional Ψ*|Ψ. The diffusion of this half-imaginary stuff is the underpinning of reality — if viewed in a certain way.

First let’s consider the steady diffusion of a normal (un-quantum) material. If there is a lot of it, like when there’s perfume off of a prima donna, you can say that N = -D dc/dx where N is the flux of perfume (molecules per minute per area), dc/dx is a concentration gradient (there’s more perfume near her than near you), and D is a diffusivity, a number related to the mobility of those perfume molecules. 

We can further generalize the diffusion of an ordinary material for a case where concentration varies with time because of reaction or a difference between the in-rate and the out rate, with reaction added as a secondary accumulator, we can write: dc/dt = reaction + dN/dx = reaction + D d2c/dx2. For a first order reaction, for example radioactive decay, reaction = -ßc, and 

dc/dt = -ßc + D d2c/dx2               (1)

where ß is the radioactive decay constant of the material whose concentration is c.

Viewed in a certain way, the most relevant equation for reality, the time-dependent Schrödinger wave equation (semi-derived here), fits into the same diffusion-reaction form:

dΨ/dt = – 2iπV/h Ψ + hi/4πm d2Ψ/dx2                (2)

Instead of reality involving the motion of a real material (perfume, radioactive radon, etc.) with a real concentration, c, in this relation, the material can not be sensed directly, and the concentration, Ψ, is semi -imaginary. Here, h is plank’s constant, i is the imaginary number, √-1, m is the mass of the real material, and V is potential energy. When dealing with reactions or charged materials, it’s relevant that V will vary with position (e.g. electrons’ energy is lower when they are near protons). The diffusivity term here is imaginary, hi/4πm, but that’s OK, Ψ is part imaginary, and we’d expect that potential energy is something of a destroyer of Ψ: the likelihood of finding something at a spot goes down where the energy is high.

The form of this diffusion is linear, a mathematical term that refers to equations where solution that works for Ψ will also work for 2Ψ. Generally speaking linear solutions have exp() terms in them, and that’s especially likely here as the only place where you see a time term is on the left. For most cases we can say that

Ψ = ψ exp(-2iπE/h)t               (3)

where ψ is not a function of anything but x (space) and E is the energy of the thing whose behavior is described by Ψ. If you take the derivative of equation 3 this with respect to time, t, you get

dΨ/dt = ψ (-2iπE/h) exp(-2iπE/h)t = (-2iπE/h)Ψ.               (4)

If you insert this into equation 2, you’ll notice that the form of the first term is now identical to the second, with energy appearing identically in both terms. Divide now by exp(-2iπE/h)t, and you get the following equation:

(E-V) ψ =  -h2/8π2m d2ψ/dx2                      (5)

where ψ can be thought of as the physical concentration in space of the timey-wimey stuff. ψ is still wibbly-wobbley, but no longer timey-wimey. Now ψ- squared is the likelihood of finding the stuff somewhere at any time, and E, the energy of the thing. For most things in normal conditions, E is quantized and equals approximately kT. That is E of the thing equals, typically, a quantized energy state that’s nearly Boltzmann’s constant times temperature.

You now want to check that the approximation in equation 3-5 was legitimate. You do this by checking if the length-scale implicit in exp(-2iπE/h)t is small relative to the length-scales of the action. If it is (and it usually is), You are free to solve for ψ at any E and V using normal mathematics, by analytic or digital means, for example this way. ψ will be wibbely-wobbely but won’t be timey-wimey. That is, the space behavior of the thing will be peculiar with the item in forbidden locations, but there won’t be time reversal. For time reversal, you need small space features (like here) or entanglement.

Equation 5 can be considered a simple steady state diffusion equation. The stuff whose concentration is ψ is created wherever E is greater than V, and is destroyed wherever V is greater than E. The stuff then continuously diffuses from the former area to the latter establishing a time-independent concentration profile. E is quantized (can only be some specific values) since matter can never be created of destroyed, and it is only at specific values of E that this happens in Equation 5. For a particle in a flat box, E and ψ are found, typically, by realizing that the format of ψ must be a sin function (and ignoring an infinity). For more complex potential energy surfaces, it’s best to use a matrix solution for ψ along with non-continuous calculous. This avoids the infinity, and is a lot more flexible besides.

When you detect a material in some spot, you can imagine that the space- function ψ collapses, but even that isn’t clear as you can never know the position and velocity of a thing simultaneously, so doesn’t collapse all that much. And as for what the stuff is that diffuses and has concentration ψ, no-one knows, but it behaves like a stuff. And as to why it diffuses, perhaps it’s jiggled by unseen photons. I don’t know if this is what happens, but it’s a way I often choose to imagine reality — a moving, unseen material with real and imaginary (spiritual ?) parts, whose concentration, ψ, is related to experience, but not directly experienced.

This is not the only way the equations can be rearranged. Another way of thinking of things is as the sum of path integrals — an approach that appears to me as a many-world version, with fixed-points in time (another Dr Who feature). In this view, every object takes every path possible between these points, and reality as the sum of all the versions, including some that have time reversals. Richard Feynman explains this path integral approach here. If it doesn’t make more sense than my version, that’s OK. There is no version of the quantum equations that will make total, rational sense. All the true ones are mathematically equivalent — totally equal, but differ in the “meaning”. That is, if you were to impose meaning on the math terms, the meaning would be totally different. That’s not to say that all explanations are equally valid — most versions are totally wrong, but there are many, equally valid math version to fit many, equally valid religious or philosophic world views. The various religions, I think, are uncomfortable with having so many completely different views being totally equal because (as I understand it) each wants exclusive ownership of truth. Since this is never so for math, I claim religion is the opposite of science. Religion is trying to find The Meaning of life, and science is trying to match experiential truth — and ideally useful truth; knowing the meaning of life isn’t that useful in a knife fight.

Dr. Robert E. Buxbaum, July 9, 2014. If nothing else, you now perhaps understand Dr. Who more than you did previously. If you liked this, see here for a view of political happiness in terms of the thermodynamics of free-energy minimization.

17+ years of no climate change

3 Replies

Much of the data underlying climate change is bad, as best I can tell, and quite a lot of the animosity surrounding climate legislation comes from the failure to acknowledge this. Our (US) government likes to show the climate increasing at 4-6°C/century, or .05°C/year, but this is based on bad data of average global temperatures, truncated conveniently to 1880, and the incorrect assumption that trends always continue — a bad idea for stock investing too. We really don’t have any good world-wide temperature going back any further the 1990s, something the Canadian ice service acknowledges (see chart below) but we do not. Worse yet, we adjust our data to correct for supposed errors.

Theory vs experiment in climate change data

Theory vs experiment in climate change data; 17 years with no change.

High quality observations begin only about 10 years ago, and since then we have seen 17+ years of no significant climate change, not the .05°C per year predicted. Our models predicted an ice-free Arctic by 2013, but we had one of the coldest winters of the century. Clearly the models are wrong. Heat can’t hide, and in particular it can’t hide in the upper atmosphere where the heat is supposed to be congregating. The predictive models were not chaotic, and weather is, but instead show regular, slow temperature rises based on predictions of past experimental data.

In Canada and Australia, the climate experts are nice enough to put confidence bars on the extrapolated data before publishing it. Some researchers are also nice enough to provide data going back further, to late Roman times when the weather was really warm, or 20,000 years ago, when we had an ice age (it’s unlikely that the ice age ended because of automobile traffic).

Canada's version of Ice coverage data. The grey part is the error bar. Canada is nice enough to admit they know relatively little of what the climate was like in the 70s and 80s. We do not.

Canada’s version of Ice coverage data. The grey part is the error bar. Canada is nice enough to admit they don’t know what it was like in the 70s and 80s. We do not.

So what’s so wrong about stopping US coal use, even if it does not cause global warming. For one, it’s bad diplomatically — it weakens us and strengthens countries that hate us (like Iran), and countries like China that burn lots of coal and really pollute the air. It also diverts the US from real air pollution and land use discussions. If you want less air pollution, perhaps nuclear is the way to go. Finally, there you have to ask, even if we could adjust the earth’s temperature at will, who would get control of the thermostat? Who would decide if this summer should be warm or cold, or who should get rains, or sun. With great power comes great headaches.

Robert Buxbaum, June 21, 2014

American education sucks, how do we succeed?

11 Replies

Despite my PhD from a top American college, Princeton University, I find I lag ordinary Europeans in languages and history. I can claim to know some math, and a little Latin and a little Greek, but in my case it’s two short friends, Manuel Ramos and Stanos Platsis. It was recently reported that one fourth of college-educated Americans did not know that the earth spun on an axis. With an education system of this sort, how is it that the US has the largest GDP, and nearly the largest per-capita GDP. We have a grosser national product than any European country despite a degree of science ignorance that would be inconceivable there.

Americans hate math.

Americans hate math.

One part of US success is imported talent, of course. We import Nobel lauriate chemists, Russian dancers, German rocket scientists…, but we don’t import that many. The majority of our immigrants are more in the wretched refuse category, and even these appear to do better here in the US than their colleagues that they left behind. Otto von Bismark once joked that, “God protects children, drunks, and the United States of America.” But I’d like to suggest that our success is based on optimism, pronia: a can-do belief in ourselves that our education provides, at least to our more creative citizens.

Most of the great successful businesses of the USA are not started by the A students, it is clear, but by the C students who develop the greatness of the little they know. Consider Colonel Harlen Sanders, founder of Kentucky Fried Chicken. He believed in the greatness of his chicken recipe, and developed to skills to sell it fast. He did not have to know astronomy, whether the earth goes round the sun. It’s an important fact, but only relevant if you can use it, as Sherlock Holmes points out. I suspect that few Europeans could use the knowledge that the earth spins productively, and suspect that the majority of those that might, lack the confidence to do so (I provide some at the end of this essay).

Benjamin Jowett. His students included the heads of 6 colleges and the head of Eaton

Benjamin Jowett, Master of Balliol College, Oxford.

A classic poem about European education describes Benjamin Jowett, shown at right. It goes: “The first come I, my name is Jowett. There is no knowledge, but that I know it. I am master of this college. What I don’t know isn’t knowledge.” Benjamin Jowett was Master of Balliol College, Oxford. By the time he died in 1893, his ex-student pallbearers included the heads of 6 colleges, and the head of Eaton. Most English heads of state and industry were his students directly or second-hand. All left university with a passing knowledge of Greek, Latin, Plato, law, science, theology, classics, math, rhetoric, logic, and grammar. Only people so educated were deemed suited to run banks or manage backward nations like India or Rhodesia. It worked for a while but showed its limitations, e.g. in the Boer Wars.

In France and continental Europe, the education system is similar, to this day ,to England’s under Jowett. There is a fixed set of knowledge and a fixed rate to learn it. Government and industry jobs go largely to those who’ve demonstrated their ability to give the fixed, correct answers to tests on this knowledge. In schools across France, the same page is turned virtually simultaneously in the every school– no student is left behind, but none jump ahead either or deviate. As new knowledge is integrated, the approved text books are updated and the correct answers are adjusted. Until then, the answers in the book are God’s truth, and those who master it can comfort themselves to have mastered the truth. The European system appears to benefit the many, providing useful skills (and useless tidbits) but it is oppressive to others with forward-thinking, imaginative minds, or who see a new truth a year before the test acknowledges it. College, it is said, “..is a place where pebbles are polished but diamonds are dimmed.” The system work well in areas that barely change like French grammar, geometry, law, and the map of Europe. It does not work so well in music, computers, or the art of war. For creative students, bright or otherwise, schooling is “another brick in the wall.” These students need learning in ‘how to get along without a teacher.’

The American approach leans, or perhaps leaned, towards independence of thought, for good or bad. American graduates can live without the teacher, but leave school knowing no language but English, knowing hardly and maths or science, and hardly any grammar. We can hardly find another country on a map, and often can’t find our own. Teachers will take incorrect answers as correct as a way to build self-esteem, so students leave with the view that there is no such thing as truth. Strangely, this model works, at least in music, engineering, and science where change is fast, creativity is king, and nature itself is a teacher. American graduate-schools are preeminent in these areas. In reading, history and math our graduates might well be described as galumphing ignorants.

Every now and again the US tries to Europeanize education. The “no child left behind” movement was a Republican-led effort to teach on the French model, at least in reading and math. It never caught on. Drugs are a popular approach to making American students less obstreperous, but they work only temporarily. Americans leave school ignorant, but not stupid; respectful of those who can do things, and suspicious of those with lengthy degrees. Without Latin, we do OK as managers of the most complex operations, relying on bumptious optimism and distain for hierarchy.

In any moment of decision, the best thing you can do is the right thing, the next bet thing is the wrong thing, and the worst thing you can do is nothing. An American attitude that sometimes blows up, but works surprisingly well at times.

Often the inability to act is worse than acting wrong.

The American-educated boss will do some damage by his ignorance but it is no more than  comes from group-think: non-truths passed as truths. America stopped burning witches far sooner than Europe, and never burned Jews. America dropped nobles quicker, and transitioned to electric lights and motor cars quicker, perhaps because we put less weight on what nobles and universities did. When dealing Europeans, we greet them in a loud, cheerful voice, appoint a subordinate to “get things done,” and get in the way until lunchtime. The Europeans are suitably appalled, both by the crassness and by the random energy.

European scholars accepted that nobility gives one a handle on leadership. This belief held back the talented, non-noble. Since religion was part of education, they accepted that state should have an established religion, Anglican, in England, Catholicism in France; scientific atheism now. They learned from the state, and accepted, that divorce was unnecessary, that homosexuality should be punished by prison or worse, In the early 60s, Turing, a brilliant mathematician and computer scientist, was chemically castrated as a way to cure his homosexuality. In America our “Yankee ingenuity,” as we call it, screwed up too, but in ways like prohibition, McCarthyism, and disco. Such screwups resolved themselves relatively fast. “Ready, fire, aim” is a European description of the American method to any problem. It’s not great, but works better than “steady as she goes.”

The best option, it seems, is when we work together with those “across the pond.” It worked well for us in WWI, WWII, and the American Revolution, benefitting from Lafayette, Baron Von Steuben, Kosciusko, etc. Heading into the world cup of football (fifa soccer) this week, we’re expected to lose badly due to our lack of talent and our general inability to pass, dribble, or strategize. Still, we’ve got enthusiasm, and we’ve got a German coach. The world’s bookies give us 0.05% odds, but our chances are 10 times that, I’d say: 5%. God protects our galumphing corn-fed ignorants when, as in the Revolution, it’s attached to European coaching.

Some businesses where it helps to know the earth spins: rocketry (military and exploratory), communication via geosynchronous satellites (they only work because the earth spins), weather prediction (the spin of hurricanes is because the earth spins), cyclone lifting. It amazes me that people ever thought everything went around the earth, by the way; Mercury and Venus never appear overhead. If authorities could have been so wrong about this for so long, what might they be wrong about today?

Dr. Robert Buxbaum, June 10, 2014 I’ve also written about ADHD on Lincoln’s Gettysburg Address, on Theodore Roosevelt, and how he survived a gun shot.

Buddhists, Hindus and dentists joke

At the dentists’ office, Buddhist and Hindu monks don’t need anesthesia to have their teeth worked on. They transcend dental medication.

It’s funny because it’s a 3 word pun, and because there is something magical about the ability of people to conquer pain through meditation.

Focussed meditation can keep you from worry and other pain.

Focused meditation can keep you from worry and some physical pain. As for thugs, that’s more controversial. It’s possible that laughter, or looking at a spot will do as much. Gahan Wilson

The types of meditation, as I understand it, are two which are four. The two are focused and non-focused. focused meditation is supposed to allow you to conquer pain, both physical and spiritual. You concentrate on your breathing, or some other rhythmic action and thought; and whenever you realize that your mind is wandering you bring it back. A popular version is called square breathing: you breath in, hold, breath out, hold, etc. In time there is a sense of calm with the world. In theory, you can transcend dental medication, but I use the normal western practice of Novocaine plus gas. Meditation practitioners claim that directed meditation can also protect you from villains and bring peace in the world; I suspect that’s true, but also suspect that humor, or staring at a spot will do as much. I suspect that Dr Seuss has done wonders for peace in the world.

The second major version of mediation is non-focused; it can bring enlightenment if you use it right. You repeat a mantra slowly and let your mind wander along some general paths. The classic incantatory mantra is OM, and the classic paths include: what am I doing with my life, imagine a stick with one end, what is the sound of a hand clapping. The enlightenment that is supposed to arise is supposed to promote non-violence, charity, and a sense of oneness with the all. In general, I’ve found that letting one’s mind wander is a great way to solve difficult problems and to help one decide whether certain situations are worth being involved with. To the extent I’ve used a mantra, it’s versions of “radiator not leaking, mind leaking,” or “computer solution not unstable, mind unstable.” In the calm of realizing there is a solution, I’ve generally been able to find a solution.

Enlightenment can be as simple as realizing that you're there already or that you shouldn't manage a country that's unlike you and dislikes you.

Enlightenment can be as simple as realizing that you’re there already.

As for the other 2 types of meditation, it depends. To some, it involves rocking to the sound of the one hand clapping (or not). To some, it’s realizing you’re there already, or that you really don’t want to get involved in an Asian war to defend and manage a country that’s completely unlike yours, and that dislikes yours as well, or that it’s OK to use Novocaine and gas when you have your teeth worked on. That’s what they are there for.

Robert E. Buxbaum, May 24, 2014. Some wisdom from the Jewish mystics: Wherever you go, there you are, as for your baggage, who knows? Tea, with the first sip joy, with the second, satisfaction, with the third, Danish.

If hot air rises, why is it cold on mountain-tops — and what of global warming?

3 Replies

This is a child’s question that’s rarely answered to anyone’s satisfaction. To answer it well requires college level science, and by college the child has usually been dissuaded from asking anything scientific that would likely embarrass teacher — which is to say, from asking most anything. By a good answer, I mean here one that provides both a mathematical, checkable prediction of the temperature you’d expect to find on mountain tops, and one that also gives a feel for why it should be so. I’ll try to provide this here, as previously when explaining “why is the sky blue.” A word of warning: real science involves mathematics, something that’s often left behind, perhaps in an effort to build self-esteem. If I do a poor job, please text me back: “if hot air rises, what’s keeping you down?”

As a touchy-feely answer, please note that all materials have internal energy. It’s generally associated with the kinetic energy + potential energy of the molecules. It enters whenever a material is heated or has work done on it, and for gases, to good approximation, it equals the gas heat capacity of the gas times its temperature. For air, this is about 7 cal/mol°K times the temperature in degrees Kelvin. The average air at sea-level is taken to be at 1 atm, or 101,300  Pascals, and 15.02°C, or 288.15 °K; the internal energy of this are is thus 288.15 x 7 = 2017 cal/mol = 8420 J/mol. The internal energy of the air will decrease as the air rises, and the temperature drops for reasons I will explain below. Most diatomic gases have heat capacity of 7 cal/mol°K, a fact that is only explained by quantum mechanics; if not for quantum mechanics, the heat capacities of diatomic gases would be about 9 cal/mol°K.

Lets consider a volume of this air at this standard condition, and imagine that it is held within a weightless balloon, or plastic bag. As we pull that air up, by pulling up the bag, the bag starts to expand because the pressure is lower at high altitude (air pressure is just the weight of the air). No heat is exchanged with the surrounding air because our air will always be about as warm as its surroundings, or if you like you can imagine weightless balloon prevents it. In either case the molecules lose energy as the bag expands because they always collide with an outwardly moving wall. Alternately you can say that the air in the bag is doing work on the exterior air — expansion is work — but we are putting no work into the air as it takes no work to lift this air. The buoyancy of the air in our balloon is always about that of the surrounding air, or so we’ll assume for now.

A classic, difficult way to calculate the temperature change with altitude is to calculate the work being done by the air in the rising balloon. Work done is force times distance: w=  ∫f dz and this work should equal the effective cooling since heat and work are interchangeable. There’s an integral sign here to account for the fact that force is proportional to pressure and the air pressure will decrease as the balloon goes up. We now note that w =  ∫f dz = – ∫P dV because pressure, P = force per unit area. and volume, V is area times distance. The minus sign is because the work is being done by the air, not done on the air — it involves a loss of internal energy. Sorry to say, the temperature and pressure in the air keeps changing with volume and altitude, so it’s hard to solve the integral, but there is a simple approach based on entropy, S.

Les Droites Mountain, in the Alps, at the intersect of France Italy and Switzerland is 4000 m tall. The top is generally snow-covered.

Les Droites Mountain, in the Alps, at the intersect of France Italy and Switzerland is 4000 m tall. The top is generally snow-covered.

I discussed entropy last month, and showed it was a property of state, and further, that for any reversible path, ∆S= (Q/T)rev. That is, the entropy change for any reversible process equals the heat that enters divided by the temperature. Now, we expect the balloon rise is reversible, and since we’ve assumed no heat transfer, Q = 0. We thus expect that the entropy of air will be the same at all altitudes. Now entropy has two parts, a temperature part, Cp ln T2/T1 and a pressure part, R ln P2/P1. If the total ∆S=0 these two parts will exactly cancel.

Consider that at 4000m, the height of Les Droites, a mountain in the Mont Blanc range, the typical pressure is 61,660 Pa, about 60.85% of sea level pressure (101325 Pa). If the air were reduced to this pressure at constant temperature (∆S)T = -R ln P2/P1 where R is the gas constant, about 2 cal/mol°K, and P2/P1 = .6085; (∆S)T = -2 ln .6085. Since the total entropy change is zero, this part must equal Cp ln T2/T1 where Cp is the heat capacity of air at constant pressure, about 7 cal/mol°K for all diatomic gases, and T1 and T2 are the temperatures (Kelvin) of the air at sea level and 4000 m. (These equations are derived in most thermodynamics texts. The short version is that the entropy change from compression at constant T equals the work at constant temperature divided by T,  ∫P/TdV=  ∫R/V dV = R ln V2/V1= -R ln P2/P1. Similarly the entropy change at constant pressure = ∫dQ/T where dQ = Cp dT. This component of entropy is thus ∫dQ/T = Cp ∫dT/T = Cp ln T2/T1.) Setting the sum to equal zero, we can say that Cp ln T2/T1 =R ln .6085, or that 

T2 = T1 (.6085)R/Cp

T2 = T1(.6085)2/7   where 0.6065 is the pressure ratio at 4000, and because for air and most diatomic gases, R/Cp = 2/7 to very good approximation, matching the prediction from quantum mechanics.

From the above, we calculate T2 = 288.15 x .8676 = 250.0°K, or -23.15 °C. This is cold enough to provide snow  on Les Droites nearly year round, and it’s pretty accurate. The typical temperature at 4000 m is 262.17 K (-11°C). That’s 26°C colder than at sea-level, and only 12°C warmer than we’d predicted.

There are three weak assumptions behind the 11°C error in our predictions: (1) that the air that rises is no hotter than the air that does not, and (2) that the air’s not heated by radiation from the sun or earth, and (3) that there is no heat exchange with the surrounding air, e.g. from rain or snow formation. The last of these errors is thought to be the largest, but it’s still not large enough to cause serious problems.

The snow cover on Kilimanjaro, 2013. If global warming models were true, it should be gone, or mostly gone.

Snow on Kilimanjaro, Tanzania 2013. If global warming models were true, the ground should be 4°C warmer than 100 years ago, and the air at this altitude, about 7°C (12°F) warmer; and the snow should be gone.

You can use this approach, with different exponents, estimate the temperature at the center of Jupiter, or at the center of neutron stars. This iso-entropic calculation is the model that’s used here, though it’s understood that may be off by a fair percentage. You can also ask questions about global warming: increased CO2 at this level is supposed to cause extreme heating at 4000m, enough to heat the earth below by 4°C/century or more. As it happens, the temperature and snow cover on Les Droites and other Alp ski areas has been studied carefully for many decades; they are not warming as best we can tell (here’s a discussion). By all rights, Mt Blanc should be Mt Green by now; no one knows why. The earth too seems to have stopped warming. My theory: clouds. 

Robert Buxbaum, May 10, 2014. Science requires you check your theory for internal and external weakness. Here’s why the sky is blue, not green.

Getting rid of hydrogen

4 Replies

Though most of my company’s business is making hydrogen or purifying it, or consulting about it, we also provide sorbers and membranes that allow a customer to get rid of unwanted hydrogen, or remove it from a space where it is not wanted. A common example is a customer who has a battery system for long-term operation under the sea, or in space. The battery or the metal containment is then found to degas hydrogen, perhaps from a corrosion reaction. The hydrogen may interfere with his electronics, or the customer fears it will reach explosive levels. In one case the customer’s system was monitoring deep oil wells and hydrogen from the well was messing up its fiber optic communications.

img505

Pd-coated niobium screws used to getter hydrogen from electronic packages.

For many of these problems, the simplest solution is an organic hydrogen getter of palladium-catalyst and a labile unsaturated hydrocarbon, e.g. buckminsterfullerene. These hydrogen getters are effective in air or inert gas at temperatures between about -20°C and 150°C. When used in an inert gas the organic is hydrogenated, there is a finite amount of removal per gram of sober. When used in air the catalyst promotes the water-forming reaction, and thus there is a lot more hydrogen removal. Depending on the organic, we can provide gettering to lower temperatures or higher. We’ve a recent patent on an organo-palladium gel to operate to 300°C, suitable for down-well hydrogen removal.

At high temperatures, generally above 100*C, we generally suggest an inorganic hydrogen remover, e.g. our platinum ceria catalyst. This material is suitable for hydrogen removal from air, including from polluted air like that in radioactive waste storage areas. Platinum catalyst works long-term at temperatures between about 0°C and 600°C. The catalyst-sorber also works without air, reducing Ce2O3 to CeO and converting hydrogen irreversibly to water (H2O). As with the organo-Pd getters, there is a finite amount of hydrogen removal per gram when these materials are used in a sealed environment.

Low temperature, Pd-grey coated, Pd-Ag membranes made for the space shuttle to remove hydrogen from the drinking water at room temperature. The water came from the fuel cells.

Low temperature, metal membranes made for NASA to remove H2 from  drinking water at room temperature.

Another high temperature hydrogen removal option is metallic getters, e.g. yttrium or vanadium-titanium alloy. These metals require temperatures in excess of 100°C to be effective, and typically do not work well in air. They are best suited for removing hydrogen a vacuum or inert gas, converting it to metallic hydride. The thermodynamics of hydriding is such that, depending on the material, these getters can extract hydrogen even at temperatures up to 700°C, and at very low hydrogen pressures, below 10-9 torr. For operation in air or at 100-400°C we typically provide these getters coated with palladium to increase the hydrogen sorption rate. A fairly popular product is palladium-coated niobium screws 4-40 x 1/4″. Each screw will remove over 2000 sec of hydrogen at temperatures up to 400°C. We also provide oxygen, nitrogen and water getters. They work on the same principle, but form metallic oxides or nitrides instead of hydrides.

Our last, and highest-end, hydrogen-removal option is to provide metallic membranes. These don’t remove the hydrogen as such, but transfer it elsewhere. We’ve provided these for the space shuttle, and to the nuclear industry so that hydrogen can be vented from nuclear reactors before it has a chance to build up and case damage or interfere with heat transfer. Because nothing is used up, these membranes work, essentially forever. The Fukushima reactor explosions were from corrosion-produced hydrogen that had no acceptable way to vent.

Please contact us for more information, e.g. by phone at 248-545-0155, or check out the various sorbers in our web-site. Robert Buxbaum, May 5, 2014.

Is ADHD a real disorder

17 Replies

When I was in school, ADHD hadn’t been invented. There were kids who didn’t pay attention for a good part of the day, or who couldn’t sit in their seats, but the first activity was called day-dreaming and the second “shpilkas” or “ants in your pants.” These problems were recognized but were considered “normal.” Though we were sometimes disorderly, the cause wasn’t labeled a disorder. It’s now an epidemic.

There were always plenty of kids, me included, who were day-dreamers. Mostly these were boys who would get bored after a while and would start to look around the room, or doodle, or gaze into space thinking of this or that. Perhaps I’d do some writing or math in the margin of a notebook while listening with one ear; perhaps I’d work on my handwriting, or I’d read something in another textbook. This was not called a disorder or even an attention deficit (AD), but rather day-dreaming, wool-gathering, napping, or just not paying attention. Sometimes teachers got annoyed, other times not. They went on teaching, but sometimes tossed chalk or erasers at us to get us to wake up. Kids like me took enough notes to do OK on tests and homework, though I was never at the top of the class in elementary or middle school. The report cards tended to say things like “he could do better if he really concentrated.”  It’s something that could apply to everyone.

Then there were the boys who would now be labeled HD, or “hyperactive disordered.” These were always boys: those who didn’t sit well in their chairs, or fidgeted, or were motor mouths and got up and walked about, or got into fights, or went to the bathroom; these were the class clowns, and the trouble makers — not me except for the fidgeting. Girls would fidget or talk too, and they’d pass notes to each other, but they didn’t get into fights, and they weren’t as disruptive. They tended to have great handwriting, and took lots of notes in class: every single word from the board, plus quite a bit more.

There are different measures of education, if you measure a fish's intelligence by the ability to climb a tree it will spend its life thinking it's stupid.

There are different measures of education, if you measure a fish’s skill level by the ability to climb a tree you’ll conclude the fish is ADD or worse.

Elementary and middle schools had activities to work out the excess energy that caused hyper-activity. We had dancing, shop, fire drills, art, some music, and sports. None of these helped all that much, but they did some good. I think the fire drills helped the most because we all went outside even in the winter, and eventually we calmed down without drugs. Sometimes a kid didn’t calm down, got worse, and did real damage; these kids were not called hyperactive disordered, but “bad kids” or “juvenile delinquents.” Nowadays, schools have far less art and music, and no shop or dancing. There are a lot more hyperactive kids, and the claim nowadays is that these hyperactive kids, violent or not, are disordered, ADHD, and should be given drugs. With drugs, the daydreamers take better notes, the nappers wake up, and the hyperactive kids calm down. Today about 30% of high-school seniors are given either a version of amphetamine, e.g. Adderall, or of Methylphenidate (Ritalin, etc.) The violent ones, the juvenile delinquents, are given stronger versions of the same drugs, e.g. methamphetamine, the drug at the heart of “breaking bad.”

Giving drugs to the kids seems to help the teacher a lot more than it helps the kids. According to a famous joke, giving the Ritalin to the teacher would be the best solution. When the kids are given drugs the disorderly boys (it’s usually given to boys) begin to act more like “goodie goodies”. They sit better and pay attention more; they take better notes and don’t interrupt, but I’m not sure they are learning more, or that the class is, or that they are socializing any better than before. The “goodie-goodies” in elementary school (mostly girls) did great in the early grades, but their good habits seemed to hold them back later. They worked too hard to please and tended to not notice, or pretended to not notice, when the teacher said nonsense. When it came time for independent or creative endeavors, their diligent acceptance of authority stood in the way of excellence.Venn diagram of ADHD

The hyperactive and daydreamers were more used to thinking for themselves, a prerequisite of leadership. The AD ones had gotten used to half-ignoring the teacher, and the HD ones were more openly opinionated and oppositional: obstreperous, in a word. Those bright enough to get by got more out of their education, perhaps because it was more theirs. To the extent that education was supposed to make you a leader and a thinker, the goodie-goodie behavior was a distraction and a disorder. This might be expected if education is supposed to be the lighting of a fire, not the filling of a pit. If everyone thinks the same, it’s a sign that few are thinking.

Map of ADHD variation with location for US kids ages 6-18, Scrips Research.

Map of ADHD variation with location for US kids ages 6-18, Scrips Research. Boys are 2-3 times more often diagnosed as ADHD; diagnosis and medication increase with grade, peaking currently in early college.

This is not to say that there is no such disorder as ADHD, or no benefit from the drugs. My sense, though, is that the label is given too widely, and that the drugs are given too freely. Today drugs are pushed on virtually any kid who’s distracted, napping or hyperactive — to all the members of the big circles in the Venn diagram above, plus to athletes and others who feign ADD to get these, otherwise illegal, performance enhancing drugs. Currently, about 10% of US kids between 6 and 18 are diagnosed ADHD and given drugs, see figure. The numbers higher for boys than girls, higher in the US than abroad, and higher as the kids progress through school. It’s estimated that about 25% of US, 12th grade boys are given amphetamine or Ritalin and its homologs. My sense is that only a small fraction of these deserve drugs, only those with severe social problems, the violent or narcoleptic: those in the smaller circles of the Venn diagram. The test should not be that the kid’s behavior improves on them. Everyone’s attention improves when taking speed. ADHD appears more as an epidemic of overworked, undertrained, underfunded teachers, and a lack of outlets, not of disordered kids, or of real learning, and real learning is never pretty or easy (on all involved).

Robert Buxbaum, April 18, 2014. In general, I think people would be happier if they’d do more art, music, dance and shop, and if they’d embrace their inner weirdo. It would also help if doctors and teachers would use words rather than initials to describe people. It’s far better to be told you’re hyperactive, or that you’re not paying attention, then to be called ADD, HD, or ADHD. There’s far more room for gradation and improvement. I’m not an expert, just an observant observer.

Dada, or it’s hard to look cool sucking on a carrot.

5 Replies

When it’s done right, Dada art is cool. It’s not confusing or preachy; it’s not out there, or sloppy; just cool. And today I found the most wonderful Dada piece: “Attention”, by Gabriel -Belladonna, shown below from “deviant art” (sorry about the water-mark).

At first glance it’s an advertisement against smoking, drinking, and eating sweets. The smoker has blackened lungs, the drinker has an enlarged liver, and the eater of sweets a diseased stomach. But something here isn’t right; the sinners are happy and young. These things are clearly bad for you but they’re enjoyable too and “cool” — Smoking is a lot cooler than sucking on a carrot.

Dada at it's best: Attention by Mio Belladonna. The sinners are happy.

Dada at it’s best: “Attention” by Dadaist Gabriel (Mio) Belladonna, 2012; image from deviant art. If I were to choose the title it would be “But it’s hard to look cool sucking on a carrot.”

At its best, Dada turns advertising and art on its head; it uses the imagery of advertising to show the shallowness of that, clearly slanted medium, or uses art-museum settings to show the narrow definition of what we’ve come to call “art”. In the above you see the balance of life- reality and the mind control of advertising.

Marcel Duchamp's fountain and "Manikken Pis" Similar idea, Manikken is better executed, IMHO.

Marcel Duchamp’s fountain and “Manikken Pis.”

Any mention of dada should also, I suppose, mention Duchamp’s fountain (at right, signed fancifully by R. Mutt). In 2004, fountain was voted “the most influential artwork of the 20th century” by a panel of artists and art historians. The basic idea was to show the slight difference between art and not-art (to be something, there has to be a non-something, as in this joke). Beyond this, the idea would be that same as for the Manikken Pis sculpture in Brussels. Duchamp’s was done with a lot less work — just by signing a “found object.” He submitted the work for exhibition in 1917, but it was rejected as not being art — proving, I guess, the point. Fountain is related to man: his life, needs, and vain ambitions; it’s sort-of beautiful, so why ain’t it art? (It has something to do with skill, I’d say.)

Duchamp designed two major surrealist exhibitions — a similar approach, but surrealism typically employs more skill and humor than Dada, with less shock. Below is another famous work of dada, Oppenheim’s fur-lined tea-cup (Breakfast in fur — see it at the Modern Museum in NYC) compared to a wonderful (and in my mind similar) surreal work, “Ruby lips” by Dali. Oppenheim made the tea-cup and spoon disgusting by making it out of a richer material, fur. That’s really cool, and sort-of shocking, even today.

Duchap's tea cup (left), and Dali's ruby lips (right). Similar ideas treated as Dada or Surreal.

Meret Oppenheim’s fur tea-cup (Breakfast in fur) and Dali’s ruby lips; the same idea (I think); dada vs surreal.

Dali’s “ruby libs” brooch took more skill than gluing fur to a cup and spoon; that adds to the humor, I’d say, but took from the shock. It’s made from real rubies and pearls: hard materials for something that should be soft; it’s sort of disgusting this way, and the message is more or less the same as Oppenheim’s, I’d say, but the message gets a little lost in the literal joke (pearly teeth, ruby lips…). I could imagine someone wearing Dali’s brooch, but no one would use the fur-lined cup. 

There is a lot of bad dada, too unfortunately, and it tends to be awful: incomprehensible, trite, or advertising. An unfortunate tendency is to collect some found pieces of garbage, and set it out in an attempt to scandalize the art world, or put down “the man” for his closed mindset. But that’s fountain, and it’s been done. A key way to tell if it’s good dada — is it cool; is it something that makes you say “Wow.” Christo’s surrounded islands certainly have the wow-cool factor, IMHO. 

Christo's wrapped Islands. Islands near Miami Beach wrapped in pink (fuscha) plastic.

Christo’s surrounded Islands: Islands near Miami Beach wrapped in pink (fuchsia) plastic.

A nice thing about Christo is that he takes it down 2 weeks or so after he makes the sculptures. Thus, the wow factor of his work never has a chance to go stale. Sorry to say, most dada stays around. Duchamp’s “fountain” sits in a museum and has grown stale, at least to me and Duchamp. What was scandalous and shocking in 1917 is passé and boring in 2014. The decline in shock is somewhat less for “breakfast in fur,” I think because the work is better crafted, a benefit I see in “Attention” too; skill matters.

Paris Street art. I don't know the artist, but it's cool.

Paris Street art; it’s just cool.

At the height of his success, Duchamp left art for 30 years and played chess. He became a chess grand master (life is as strange as art) and played for France in international tournaments. He later came back to art and did one, last, final piece, a very fine one, seen only through a peephole. Here’s some further thoughts on good vs bad modern art, and on surrealism, and on the aesthetic of strength in engineering: what materials to use; how strong should it be, and on architecture humor. 

Robert E. Buxbaum. April 4-7, 2014. Here is a link to my attempt at good Dada: Kilroy with eyes that follow you, and at right some Paris street art that I consider good dada too. As far as what the word “dada” means, I translate it as “cool,” “wow,” “gnarly,” or “go go.” It’s dada, man, y’ dig?

Seeing entropy, the most important pattern in life

17 Replies

One evening at the Princeton grad college a younger fellow (an 18-year-old genius) asked the most simple, elegant question I had ever heard, one I’ve used ever since: “tell me”, he asked, “something that’s important and true.” My answer was that the entropy of the universe is always increasing. It’s a fundamentally important pattern, one I discovered to have a lot of applications and meaning. Let me explain the concept and why it’s true and useful. After that, why I find it’s meaningful.

Famous entropy cartoon, Harris

Famous entropy cartoon, Harris

The entropy of the universe is not something you can measure directly, but indirectly, from the availability of work in any corner of it. It’s related to randomness and the arrow of time. If you have, for example, an ice cube and a hot cup of water, you can get useful work from these by way of a thermocouple placed between them. You’ll get work until the two are at the same temperature. To get useful work out, you’ll have to add some other item.

Now, here’s how you can tell if time is moving forward: put an ice-cube into hot water, if the cube dissolves and the water becomes cooler, time is moving forward — or, at least it’s moving in the same direction as you are. If you can reach into a cup of warm water and pull out an ice-cube while making the water hot, time is moving backwards. — or rather, you are living backwards. Within any closed system, one where you don’t add things or energy (sunlight say), you can tell that time is moving forward because the forward progress of time always leads to the lack of availability of work. In the case above, you generated some electricity from the ice-cube and the hot water, but could not from the glass of warm water at the end.

You can not extract work from a heat source alone; to extract work some heat must be deposited in a cold sink. At best the entropy of the universe remains unchanged. More typically, it increases.

You can not extract work from a heat source alone; to extract work some heat must be deposited in a cold sink. At best the entropy of the universe remains unchanged.

This observation is about as general and fundamental as any to understanding the world; it is the basis of the second law of thermodynamics: you can never extract useful work from a uniform temperature item, by making that item cooler say. To get useful work, you always need to make something else hotter, or colder, or you have to provide some chemical, altitude or other change that can not be reversed without adding more energy back. Thus, so long as time moves forward, everything “runs down” in terms of work availability.

The concept of entropy is the result of this observation along with another observation that energy is conserved. That is, if you want to heat some uniform substance, you must put in work and/or heat in any combination. And, if you want to cool something back to the original state, that same amount of heat + work must be taken out. In equation form, we say that, for any change, q +w is constant, where q is heat, and w is work. It’s the sum that’s constant, not the individual values so long as you count every 4.174 Joules of work as if it were 1 calorie of heat. If you input more heat, you have to add less work, and visa versa, but it’s always the same sum. When adding heat or work to the substance, we say that q or w is positive; when extracting heat or work, we say that q or w are negative quantities. So long as each 4.174 joules counts as if it were 1 calorie you get the same temperature change. This conservation of energy observation is called the first law of thermodynamics.

Now, since for every path between two states, q +w is the same, we say that q + w represents a path-independent quantity for the system, one we call internal energy, U where ∆U = q + w. This is a mathematical form of the first law of thermodynamics: you can’t take q + w out of nothing, or add it to something without making a change in the properties of the thing. The only way to leave things the same is if q + w = 0. We notice also that for any pure thing or uniform mixture undergoing a temperature change, the sum q +w that is needed to make that temperature change is proportional to the mass of the stuff. We can thus say that internal energy is an intensive quality. q + w = n ∆u where n is the grams of material, and ∆u is the change in internal energy per gram.

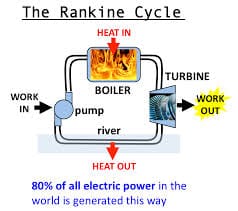
We are now ready to put the first and second laws together. We find we can extract work from a system if we take heat from a hot body (the hot water, say) and deliver some of it to something at a lower temperature (the ice-cube say). This can be done with a thermocouple, as above, or with a steam engine (Rankine cycle, shown above), or a Sterling engine, etc. These engines extract work only when there is a difference of temperatures. It’s is similar to a water wheel: a water wheel can extract work only when there is a flow of water from a high level to low; similarly in a heat engine, you only get work by taking heat energy from a hot heat-source and exhausting some of it to at a lower temperature. The remainder of that heat energy leaves the engine as work. That is, q1 -q2 = w. energy is always conserved. If you returned the amount of heat and work, you could return the hot source to its original condition. The second law isn’t violated either; there is no way you could run the engine without the cold sink. Accepting this as reasonable, we can now derive some very interesting, non-obvious truths.

We begin with the famous Carnot cycle. The Carnot cycle is an idealized heat engine with the interesting feature that it can be made to operate reversibly. That is, you can make it run forwards, taking a certain amount of work from a hot source, producing a certain amount of work and delivering a certain amount of heat to the cold sink; and you can run the same process backwards, as a refrigerator, taking in the same about of work and the same amount of heat from the cold sink and delivering the same amount to the hot source. Carnot showed by the following proof that all other reversible engines would have the same efficiency as his cycle and no engine, reversible or not, could be more efficient. The proof: if an engine could be designed that will extract a greater percentage of the heat as work when operating between a given hot source and cold sink it could be used to drive his Carnot cycle backwards. If the pair of engines were now combined so that the less efficient engine removed exactly as much heat from the sink as the more efficient engine deposited, the excess work produced by the more efficient engine would leave with no effect besides cooling the source. This combination would be in violation of the second law, something that we’d said was impossible.

Now let us try to understand the relationship that drives useful energy production. The ratio of heat in to heat out has got to be a function of the in and out temperatures alone. That is, q1/q2 = f(T1, T2). Similarly, q2/q1 = f(T2,T1) Now lets consider what happens when two Carnot cycles are placed in series between T1 and T2, with the middle temperature at Tm. For the first engine, q1/qm = f(T1, Tm), and similarly for the second engine qm/q2 = f(Tm, T2). Combining these we see that q1/q2 = (q1/qm)x(qm/q2) and therefore f(T1, T2) must always equal f(T1, Tm)x f(Tm/T2) =f(T1,Tm)/f(T2, Tm). In this relationship we see that the second term Tm is irrelevant; it is true for any Tm. We thus say that q1/q2 = T1/T2, and this is the limit of what you get at maximum (reversible) efficiency. You can now rearrange this to read q1/T1 = q2/T2 or to say that work, W = q1 – q2 = q2 (T1 – T2)/T2.

A strange result from this is that, since every process can be modeled as either a sum of Carnot engines, or of engines that are less-efficient, and since the Carnot engine will produce this same amount of reversible work when filled with any substance or combination of substances, we can say that this outcome: q1/T1 = q2/T2 is independent of path, and independent of substance so long as the process is reversible. We can thus say that for all substances there is a property of state, S such that the change in this property is ∆S = ∑q/T for all the heat in or out. In a more general sense, we can say, ∆S = ∫dq/T, where this state property, S is called the entropy. Since as before, the amount of heat needed is proportional to mass, we can say that S is an intensive property; S= n s where n is the mass of stuff, and s is the entropy change per mass. 

Another strange result comes from the efficiency equation. Since, for any engine or process that is less efficient than the reversible one, we get less work out for the same amount of q1, we must have more heat rejected than q2. Thus, for an irreversible engine or process, q1-q2 < q2(T1-T2)/T2, and q2/T2 is greater than -q1/T1. As a result, the total change in entropy, S = q1/T1 + q2/T2 >0: the entropy of the universe always goes up or stays constant. It never goes down. Another final observation is that there must be a zero temperature that nothing can go below or both q1 and q2 could be positive and energy would not be conserved. Our observations of time and energy conservation leaves us to expect to find that there must be a minimum temperature, T = 0 that nothing can be colder than. We find this temperature at -273.15 °C. It is called absolute zero; nothing has ever been cooled to be colder than this, and now we see that, so long as time moves forward and energy is conserved, nothing will ever will be found colder.

Typically we either say that S is zero at absolute zero, or at room temperature.

We’re nearly there. We can define the entropy of the universe as the sum of the entropies of everything in it. From the above treatment of work cycles, we see that this total of entropy always goes up, never down. A fundamental fact of nature, and (in my world view) a fundamental view into how God views us and the universe. First, that the entropy of the universe goes up only, and not down (in our time-forward framework) suggests there is a creator for our universe — a source of negative entropy at the start of all things, or a reverser of time (it’s the same thing in our framework). Another observation, God likes entropy a lot, and that means randomness. It’s his working principle, it seems.

But before you take me now for a total libertine and say that since science shows that everything runs down the only moral take-home is to teach: “Let us eat and drink,”… “for tomorrow we die!” (Isaiah 22:13), I should note that his randomness only applies to the universe as a whole. The individual parts (planets, laboratories, beakers of coffee) does not maximize entropy, but leads to a minimization of available work, and this is different. You can show that the maximization of S, the entropy of the universe, does not lead to the maximization of s, the entropy per gram of your particular closed space but rather to the minimization of a related quantity µ, the free energy, or usable work per gram of your stuff. You can show that, for any closed system at constant temperature, µ = h -Ts where s is entropy per gram as before, and h is called enthalpy. h is basically the potential energy of the molecules; it is lowest at low temperature and high order. For a closed system we find there is a balance between s, something that increases with increased randomness, and h, something that decreases with increased randomness. Put water and air in a bottle, and you find that the water is mostly on the bottom of the bottle, the air is mostly on the top, and the amount of mixing in each phase is not the maximum disorder, but rather the one you’d calculate will minimize µ.

As the protein folds its randomness and entropy decrease, but its enthalpy decreases too; the net effect is one precise fold that minimizes µ.

As a protein folds its randomness and entropy decrease, but its enthalpy decreases too; the net effect is one precise fold that minimizes µ.

This is the principle that God applies to everything, including us, I’d guess: a balance. Take protein folding; some patterns have big disorder, and high h; some have low disorder and very low h. The result is a temperature-dependent  balance. If I were to take a moral imperative from this balance, I’d say it matches better with the sayings of Solomon the wise: “there is nothing better for a person under the sun than to eat, drink and be merry. Then joy will accompany them in their toil all the days of the life God has given them under the sun.” (Ecclesiastes 8:15). There is toil here as well as pleasure; directed activity balanced against personal pleasures. This is the µ = h -Ts minimization where, perhaps, T is economic wealth. Thus, the richer a society, the less toil is ideal and the more freedom. Of necessity, poor societies are repressive. 

Dr. Robert E. Buxbaum, Mar 18, 2014. My previous thermodynamic post concerned the thermodynamics of hydrogen production. It’s not clear that all matter goes forward in time, by the way; antimatter may go backwards, so it’s possible that anti matter apples may fall up. On microscopic scale, time becomes flexible so it seems you can make a time machine. Religious leaders tend to be anti-science, I’ve noticed, perhaps because scientific miracles can be done by anyone, available even those who think “wrong,” or say the wrong words. And that’s that, all being heard, do what’s right and enjoy life too: as important a pattern in life as you’ll find, I think. The relationship between free-energy and societal organization is from my thesis advisor, Dr. Ernest F. Johnson.