Category Archives: REB Research products

Low temperature hydrogen removal

Leave a reply

Platinum catalysts can be very effective at removing hydrogen from air. Platinum promotes the irreversible reaction of hydrogen with oxygen to make water: H2 + 1/2 O2 –> H2O, a reaction that can take off, at great rates, even at temperatures well below freezing. In the 1800s, when platinum was cheap, platinum powder was used to light town-gas, gas street lamps. In those days, street lamps were not fueled by methane, ‘natural gas’, but by ‘town gas’, a mix of hydrogen and carbon monoxide and many impurities like H2S. It was made by reacting coal and steam in a gas plant, and it is a testament to the catalytic power of Pt that it could light this town gas. These impurities are catalytic poisons. When exposed to any catalyst, including platinum, the catalyst looses it’s power to. This is especially true at low temperatures where product water condenses, and this too poisons the catalytic surface.

Nowadays, platinum is expensive and platinum catalysts are no longer made of Pt powder, but rather by coating a thin layer of Pt metal on a high surface area substrate like alumina, ceria, or activated carbon. At higher temperatures, this distribution of Pt improves the reaction rate per gram Pt. Unfortunately, at low temperatures, the substrate seems to be part of the poisoning problem. I think I’ve found a partial way around it though.

My company, REB Research, sells Pt catalysts for hydrogen removal use down to about 0°C, 32°F. For those needing lower temperature hydrogen removal, we offer a palladium-hydrocarbon getter that continues to work down to -30°C and works both in air and in the absence of air. It’s pretty good, but poisons more readily than Pt does when exposed to H2S. For years, I had wanted to develop a version of the platinum catalyst that works well down to -30°C or so, and ideally that worked both in air and without air. I got to do some of this development work during the COVID downtime year.

My current approach is to add a small amount of teflon and other hydrophobic materials. My theory is that normal Pt catalysts form water so readily that the water coats the catalytic surface and substrate pores, choking the catalyst from contact with oxygen or hydrogen. My thought of why our Pd-organic works better than Pt is that it’s part because Pd is a slower water former, and in part because the organic compounds prevent water condensation. If so, teflon + Pt should be more active than uncoated Pt catalyst. And it is so.

Think of this in terms of the  Van der Waals equation of state:{\displaystyle \left(p+{\frac {a}{V_{m}^{2}}}\right)\left(V_{m}-b\right)=RT}

where V_{m} is molar volume. The substance-specific constants a and b can be understood as an attraction force between molecules and a molecular volume respectively. Alternately, they can be calculated from the critical temperature and pressure as

{\displaystyle a={\frac {27(RT_{c})^{2}}{64p_{c}}}}{\displaystyle b={\frac {RT_{c}}{8p_{c}}}.}

Now, I’m going to assume that the effect of a hydrophobic surface near the Pt is to reduce the effective value of a. This is to say that water molecules still attract as before, but there are fewer water molecules around. I’ll assume that b remains the same. Thus the ratio of Tc and Pc remains the same but the values drop by a factor of related to the decrease in water density. If we imagine the use of enough teflon to decrease he number of water molecules by 60%, that would be enough to reduce the critical temperature by 60%. That is, from 647 K (374 °C) to 359 K, or -14°C. This might be enough to allow Pt catalysts to be used for H2 removal from the gas within a nuclear wast casket. I’m into nuclear, both because of its clean power density and its space density. As for nuclear waste, you need these caskets.

I’ve begun to test of my theory by making hydrogen removal catalyst that use both platinum and palladium along with unsaturated hydrocarbons. I find it works far better than the palladium-hydrocarbon getter, at least at room temperature. I find it works well even when the catalyst is completely soaked in water, but the real experiments are yet to come — how does this work in the cold. Originally I planned to use a freezer for these tests, but I now have a better method: wait for winter and use God’s giant freezer.

Robert E. Buxbaum October 20, 2021. I did a fuller treatment of the thermo above, a few weeks back.

Weird thermodynamics near surfaces can prevent condensation and make water more slippery.

2 Replies

It is a fundamental of science that that the properties of every pure one-phase material is totally fixed properties at any given temperature and pressure. Thus for example, water at 0°C is accepted to always have a density of 0.998 gm/cc, a vapor pressure of 17.5 Torr, a viscosity of 1.002 centipoise (milliPascal seconds) and a speed of sound of 1481 m/s. Set the temperature and pressure of any other material and every other quality is set. But things go screwy near surfaces, and this is particularly true for water where the hydrogen bond — a quantum bond — predominates.

its vapor pressure rises and it becomes less inclined to condense or freeze. I use this odd aspect of thermodynamics to keep my platinum-based hydrogen getter catalysis active at low temperatures where they would normally clog. Normal platinum catalysts are not suitable for hydrogen removal at normal temperatures, eg room temperature, because the water that forms from hydrogen oxidation chokes off the catalytic surface. Hydrophobic additions prevent this, and I’d like to show you why this works, and why other odd things happen, based on an approximation called the  Van der Waals equation of state:

{\displaystyle \left(p+{\frac {a}{V_{m}^{2}}}\right)\left(V_{m}-b\right)=RT} (1)

This equation described the molar volume of a pure material, V_{m}, of any pure material based not the pressure, the absolute temperature (Kelvin) and two, substance-specific constants, a and b. These constants can be understood as an attraction force term, and a molecular volume respectively. It is common to calculate a and b from the critical temperature and pressure as follows, where Tc is absolute temperature:

{\displaystyle a={\frac {27(RT_{c})^{2}}{64p_{c}}}}, {\displaystyle b={\frac {RT_{c}}{8p_{c}}}.} (2 a,b)

For water Tc = 647 K (374°C) and 220.5 bar. Plugging in these numbers, the Van der Waals gives reasonable values for the density of water both as a liquid and a gas, and thus gives a reasonable value for the boiling point.

Now consider the effect that an inert surface would have on the effective values of a and b near that surface. The volume of the molecules will not change, and thus b will not change, but the value of a will change, likely by about half. This is because, the number of molecules surrounding any other molecule is reduced by about half while the inert surface adds nothing to the attraction. Near a surface, surrounding molecules still attract each other the same as before, but there are about half as many molecules at any temperature and pressure.

To get a physical sense of what the surface does, consider using the new values of a and b to determine a new value for Tc and Pc, for materials near the surface. Since b does not change, we see that the presence of a surface does not affect the ratio of Tc and Pc, but it decreases the effective value of Tc — by about half. For water, that is a change from 647 K to 323.5K, 50.5°C, very close to room temperature. Pc changes to 110 bar, about 1600 psi. Since the new value of Tc is close to room temperature, the the density of water will be much lower near the surface, and the viscosity can be expected to drop. The net result is that water flows more readily through a teflon pipe than through an ordinary pipe, a difference that is particularly apparent at small diameters.

This decrease in effective Tc is useful for fire hoses, and for making sailing ships go faster (use teflon paint) and for making my hydrogen removal catalysts more active at low temperatures. Condensed water can block the pores to the catalyst; teflon can forestall this condensation. It’s a general trick of thermodynamics, reasonably useful. Now you know it, and now you know why it works.

Robert Buxbaum August 30, 2021

Alice’s Restaurant and Nuclear Waste

Leave a reply

It’s not uncommon for scientists to get inspiration from popular music. I’d already written about how the song ‘City of New Orleans’ inspires my view of the economics of trains, I’d now like to talk about dealing with nuclear waste, and how the song Alice’s Restaurant affects my outlook.

As I see it, nuclear power is the elephant in the room in terms of clean energy. A piece of uranium the size of a pencil eraser produces as much usable energy as three rail cars of coal. There is no air pollution and the land use is far less than for solar or wind power. The one major problem was what to do with the left over eraser-worth of waste. Here’s the song, it’s 18 1/2 minutes long. The key insight appeared in the sixth stanza: “…at the bottom of the cliff there was another pile of garbage. And we decided that one big pile Is better than two little piles…”

The best way to get rid of nuclear waste would be (as I’ve blogged) to use a fast nuclear reactor to turn the worst components into more energy and less-dangerous elements. Unfortunately doing this requires reprocessing, and reprocessing was banned by Jimmy Carter, one of my least favorite presidents. The alternative is to store the nuclear waste indefinitely, waiting for someone to come up with a solution, like allowing it to be buried in Yucca Mountain, the US burial site that was approved, but that Obama decided should not be used. What then? We have nuclear waste scattered around the country, waiting. I was brought in as part of a think-tank, to decide what to do with it, and came to agree with several others, and with Arlo Guthrie, that one big pile [of waste] Is better than two little piles. Even if we can’t bury it, it would be better to put the waste in fewer places (other countries bury their waste, BTW).

That was many years ago, but even the shipping of waste has been held up as being political. Part of the problem is that nuclear waste gives off hydrogen — the radiation knocks hydrogen atoms off of water, paper, etc. and you need to keep the hydrogen levels low to be able to transport the waste safely. As it turns out we are one a few companies that makes hydrogen removal pellets and catalysts. Our products have found customers running tourist submarines (lead batteries also give off hydrogen) and customers making sealed electronics, and we are waiting for the nuclear shipping industry to open up. In recent months, I’ve been working on improving our products so they work better at low temperature. Perhaps I’ll write about that later, but here’s where you’d go to buy our current products.

Robert Buxbaum, July 4, 2021. I’ve done a few hydrogen-related posts in a row now. In part that’s because I’d noticed that I went a year or two talking history and politics, and barely talking about H2. I know a lot about hydrogen — that’s my business– as for history or politics, who knows.

Adding H2 to an engine improves mpg, lowers pollution.

1 Reply

I month ago, I wrote to endorse hythane, a mix of natural gas (methane) and 20-40% hydrogen. This mix is ideal for mobile use in solid oxide fuel cell vehicles, and not bad with normal IC engines. I’d now like to write about the advantages of an on-broad hydrogen generator to allow adjustable composition fuel mixes.

A problem you may have noticed with normal car engines is that a high hp engine will get lower miles per gallon, especially when you’re driving slow. That seems very strange; why should a bigger engine use more gas than a dinky engine, and why should you get lower mpg when you drive slow. The drag force on a vehicle is proportional to speed squared. You’d expect better milage at low speeds– something that textbooks claim you will see, counter to experience.

Behind these two problems are issues of fuel combustion range and pollution. You can solve both issues with hydrogen. With normal gasoline or Diesel engines, you get more or less the same amount of air per engine rotation at all rpm speeds, but the amount of air is much higher for big engines. There is a relatively small range of fuel-air mixes that will burn, and an even smaller range that will burn at low pollution. You have to add at least the minimal fuel per rotation to allow the engine to fire. For most driving that’s the amount the carburetor delivers. Because of gearing, your rpm is about the same at all speeds, you use almost the same rate of fuel at all speeds, with more fuel used in big engines. A gas engine can run lean, but normally speaking it doesn’t run at all any leaner than about 1.6 times the stoichiometric air-to-fuel mix. This is called a lambda of 1.6. Adding hydrogen extends the possible lambda range, as shown below for a natural gas – fired engine.

Engine efficiency when fueled with natural gas plus hydrogen as a function of hydrogen amount and lambda, the ratio of air to stoichiometric air.

The more hydrogen in the mix the wider the range, and the less pollution generally. Pure hydrogen burns at ten times stoichiometric air, a lambda of ten. There is no measurable pollution there, because there is no carbon to form CO, and temperature is so low that you don’t form NOx. But the energy output per rotation is low (there is not much energy in a volume of hydrogen) and hydrogen is more expensive than gasoline or natural gas on an energy basis. Using just a little hydrogen to run an engine at low load may make sense, but the ideal mix of hydrogen and ng fuel will change depending on engine load. At high load, you probably want to use no hydrogen in the mix.

As it happens virtually all of most people’s driving is at low load. The only time when you use the full horse-power is when you accelerate on a highway. An ideal operation for a methane-fueled car would add hydrogen to the carburetor intake at about 1/10 stoichiometric when the car idles, turning down the hydrogen mix as the load increases. REB Research makes hydrogen generators based on methanol reforming, but we’ve yet to fit one to a car. Other people have shown that adding hydrogen does improve mpg.

Carburetor Image from a course “Farm Power”. See link here. Adding hydrogen means you could use less gas.

Adding hydrogen plus excess air means there is less pollution. There is virtually no CO at idle because there is virtually no carbon, and even at load because combustion is more efficient. The extra air means that combustion is cooler, and thus you get no NOx or unburned HCs, even without a catalytic converter. Hydrogen is found to improve combustion speed and extent. A month ago, I’d applied for a grant to develop a hydrogen generator particularly suited to methane engines. Sorry to say, the DoT rejected my proposal.

Robert Buxbaum June 24, 2021

Upgrading landfill and digester gas for sale, methanol

Leave a reply

We live in a throw-away society, and the majority of it, eventually makes its way to a landfill. Books, food, grass clippings, tree-products, consumer electronics; unless it gets burnt or buried at sea, it goes to a landfill and is left to rot underground. The product of this rot is a gas, landfill gas, and it has a fairly high energy content if it could be tapped. The composition of landfill gas changes, but after the first year or so, the composition settles down to a nearly 50-50 mix of CO2 and methane. There is a fair amount of water vapor too, plus some nitrogen and hydrogen, but the basic process is shown below for wood decomposition, and the products are CO2  and methane.

System for sewage gas upgrading, uses REB membranes.

C6 H12 O6  –> 3 CO2  + 3 CH4 

This mix can not be put in the normal pipeline: there is too much CO2  and there are too many other smelly or condensible compounds (water, methanol, H2S…). This gas is sometimes used for heat on site, but there is a limited need for heat near a landfill. For the most part it is just vented or flared off. The waste of a potential energy source is an embarrassment. Besides, we are beginning to notice that methane causes global-warming with about 50 times the effect of CO2, so there is a strong incentive to capture and burn this gas, even if you have no use for the heat. I’d like to suggest a way to use the gas.

We sell small membrane modules too.

The landfill gas can be upgraded by removing the CO2. This can be done via a membrane, and REB Research sells a membranes that can do this. Other companies have other membranes that can do this too, but ours are smaller, and more suitable to small operations in my opinion. Our membrane are silicone-based. They retain CH4 and CO and hydrogen, while extracting water, CO2 and H2S, see schematic. The remainder is suited for local use in power generation, or in methanol production. It can also be used to run trucks. Also the gas can be upgraded further and added to a pipeline for shipping elsewhere. The useless parts can be separated for burial. Find these membranes on the REB web-site under silicone membranes.

Garbage trucks in New York powered by natural gas. They could use landfill gas.

There is another gas source whose composition is nearly identical to that of landfill gas; it’s digester gas, the output of sewage digesters. I’ve written about sewage treatment mostly in terms of aerobic bio treatment, for example here, but sewage can be treated anaerobically too, and the product is virtually identical to landfill gas. I think it would be great to power garbage trucks and buses with this. Gas. In New York, currently, some garbage trucks are powered by natural gas.

As a bonus, here’s how to make methanol from partially upgraded landfill or digester gas. As a first step 2/3 of the the CO2 removed. The remained will convert to methanol. by the following overall chemistry:

3 CH4 + CO2 + 2 H2O –> 4 CH3OH. 

When you removed the CO2., likely most of the water will leave with it. You add back the water as steam and heat to 800°C over Ni catalyst to make CO and H2. That’s done at about 800°C and 200 psi. Next, at lower temperature, with an appropriate catalyst you recombine the CO and H2 into methanol; with other catalysts you can make gasoline. These are not trivial processes, but they are doable on a smallish scale, and make economic sense where the methane is essentially free and there is no CNG customer. Methanol sells for $1.65/gal when sold by the tanker full, but $5 to $10/gal at the hardware store. That’s far higher than the price of methane, and methanol is far easier to ship and sell in truckload quantities.

Robert Buxbaum, June 8, 2021

Blue diamonds, natural and CVD.

Leave a reply
The hope diamond resides in the Smithsonian. It really is a deep blue. It has about 5 ppm boron.

If you’ve ever seen the Hope Dimond, or a picture of it, you’ll notice a most remarkable thing: it is deep blue. While most diamonds are clear, or perhaps grey, a very few are colored. Color in diamonds is generally caused by impurities, in the case of blue diamonds, boron. The Hope diamond has about 5 ppm boron, making it a p-semiconductor. Most blue diamonds, even those just as blue, have less boron. As it turns out one of the major uses of my hydrogen purifiers hydrogen these days is in the manufacture of gem -quality, and semiconductor diamonds, some blue and some other colors. So I thought I’d write about diamonds, colored and not, natural and CVD. It’s interesting and a sort of plug for my company, REB Research.

To start off, natural diamond are formed, over centuries by the effect of high temperature and pressure on a mix of carbon and a natural catalyst mineral, Kimberlite. Diamonds formed this way are generally cubic, relatively clear, and inert, hard, highly heat conductive, and completely non-conducting of electricity. Some man made diamonds are made this way too, using high pressure presses, but gem-quality and semiconductor diamonds are generally made by chemical vapor deposition, CVD. Colored diamonds are made this way too. They have all the properties of clear diamonds, but they have controlled additions and imperfections. Add enough boron, 1000 ppm for example, and the diamond and the resulting blue diamond can conduct electricity fairly readily.

gif2
Seeds of natural diamond are placed in a diamond growth chamber and heated to about 1000°C in the presence of ionized, pure methane and hydrogen.

While natural diamond are sometimes used for technical applications, e.g. grind wheels, most technical-use diamonds are man-made by CVD, but the results tend to come out yellow. This was especially true in the early days of manufacture. CVD tends to make large, flat diamonds. This is very useful for heat sinks, and for diamond knives and manufacturers of these were among my first customers. To get a clear color, or to get high-quality colored diamonds, you need a mix of high purity methane and high purity hydrogen, and you need to avoid impurities of silica and the like from the diamond chamber. CVD is also used to make blue-conductive diamonds that can be used as semiconductors or electrodes. The process is show in the gif above from “brilliantearth”.

Multicolored diamonds made by CVD with many different dopants and treatments.

To make a CVD diamond, you place 15 to 30 seed- diamonds into a vacuum growth chamber with a flow of methane and hydrogen in ratio of 1:100 about. You heat the gas to about 1000°C (900-1200°C) , while ionizing the gas using microwaves or a hot wire. The diamonds grow epitaxially over the course of several days or weeks. Ionized hydrogen keeps the surface active, while preventing it from becoming carbonized — turning to graphite. If there isn’t enough hydrogen, you get grey, weak diamonds. If the gas isn’t pure, you get inclusions that make them appear yellow or brown. Nitrogen-impure diamonds are n-semiconductors, with a band gap greater than with boron-blue diamonds, 0.5-1 volts more. Because of this difference, nitrogen-impure diamonds absorb blue or green light, making them appear yellow, while blue diamonds absorb red light, making them blue. (This is different from the reason the sky is blue, explained here.) The difference in energy, also makes yellow diamonds poor electrical conductors. Natural, nitrogen-impure diamonds fluoresce blue or green, as one might expect, but yellow diamonds made by CVD fluoresce at longer wavelengths, reddish (I don’t know why).

The blue moon diamond, it is about as blue as the hope diamond though it has only 0.36 ppm of boron.

To make a higher-quality, yellow, n-type CVD diamonds, use very pure hydrogen. Bright yellow and green color is added by use of ppm-quantities of sulfur or phosphorus. Radiation damage also can be used to add color. Some CVD diamond makers use heat treatment to modify the color and reduce the amount of red fluorescence. CVD pink and purple diamonds are made by hydrogen doping, perhaps followed by heat treatment. The details are proprietary secrets.


Orange-red phosphorescence in the blue moon diamond.

Two major differences help experts distinguish between natural and man-made diamonds. One of these is the fluorescence, Most natural diamonds don’t fluoresce at all, and the ones that do (about 25%) fluoresce blue or green. Almost all CVD diamonds fluoresce orange-red because of nitrogen impurities that absorb blue lights. If you use very pure, nitrogen-free hydrogen, you get clear diamonds avoid much of the fluorescence and yellow. That’s why diamond folks come to us for hydrogen purifiers (and generators). There is a problem with blue diamonds, in that both natural and CVD-absorb and emit red light (that’s why they appear blue). Fortunately for diamond dealers, there is a slight difference in the red emission spectrum between natural and CVD blue diamonds. The natural ones show a mix of red and blue-green. Synthetic diamonds glow only red, typically at 660 nm.

Blue diamonds would be expected to fluoresce red, but instead they show a delayed red fluorescence called phosphorescence. That is to say, when exposed to light, they glow red and continue to glow for 10-30 seconds after the light is turned off. The decay time varies quite a lot, presumably due to differences in the n and p sites.

Natural diamond photographed between polarizers show patterns that radiate from impurities.

Natural and CVD also look different when placed between crossed polarizers. Natural diamonds show multiple direction stress bands, as at left, often radiating from inclusions. CVD diamonds show fine-grained patterns or none at all (they are not made under stress), and man-made, compression diamonds show an X-pattern that matches the press-design, or no pattern at all. If you are interested in hydrogen purifiers, or pure hydrogen generators, for this or any other purposes, please consider REB Research. If you are interested in buying a CVD diamond, there are many for sale, even from deBeers.

Robert Buxbaum, October 19, 2020. The Hope diamond was worn by three French kings, by at least one British king, and by Miss Piggy. A CVD version can be worn by you.

A hydrogen permeation tester

1 Reply

Over the years I’ve done a fair amount of research on hydrogen permeation in metals — this is the process of the gas dissolving in the metal and diffusing to the other side. I’ve described some of that, but never the devices that measure the permeation rate. Besides, my company, REB Research, sells permeation testing devices, though they are not listed on our site. We recently shipped one designed to test hydrogen permeation through plastics for use in light weight hydrogen tanks, for operation at temperatures from -40°C to 85°C. Shortly thereafter we got another order for a permeation tester. With all the orders, I thought I’d describe the device a bit — this is the device for low permeation materials. We have a similar, but less complex design for high permeation rate material.

Shown below is the central part of the device. It is a small volume that can be connected to a high vacuum, or disconnected by a valve. There is an accurate pressure sensor, accurate to 0.01 Torr, and so configured that you do not get H2 + O2 reactions (something that would severely throw off results). There is also a chamber for holding a membrane so one side is help in vacuum, in connection to the gauge, and the other is exposed to hydrogen, or other gas at pressures up to 100 psig (∆P =115 psia). I’d tested to 200 psig, but currently feel like sticking to 100 psig or less. This device gives amazingly fast readings for plastics with permeabilities as low as 0.01 Barrer.

REB Research hydrogen permeation tester cell with valve and pressure sensor.

REB Research hydrogen permeation tester cell with valve and pressure sensor.

To control the temperature in this range of interest, the core device shown in the picture is put inside an environmental chamber, set up as shown below, with he control box outside the chamber. I include a nitrogen flush device as a safety measure so that any hydrogen that leaks from the high pressure chamber will not build up to reach explosive limits within the environmental chamber. If this device is used to measure permeation of a non-flammable gas, you won’t need to flush the environmental chamber.

I suggest one set up the vacuum pump right next to the entrance of the chamber; in the case of the chamber provided, that’s on the left as shown with the hydrogen tank and a nitrogen tank to the left of the pump. I’ve decided to provide a pressure sensor for the N2 (nitrogen) and a solenoidal shutoff valve for the H2 (hydrogen) line. These work together as a safety feature for long experiments. Their purpose is to automatically turn off the hydrogen if the nitrogen runs out. The nitrogen flush part of this process is a small gauge copper line that goes from the sensor into the environmental chamber with a small, N2 flow bleed valve at the end. I suggest setting the N2 pressure to 25-35 psig. This should give a good inert flow into the environmental chamber. You’ll want a nitrogen flush, even for short experiments, and most experiments will be short. You may not need an automatic N2 sensor, but you’ll be able to do this visually.

Basic setup for REB permeation tester and environmental chamber

Basic setup for REB permeation tester and environmental chamber

I shipped the permeation cell comes with some test, rubbery plastic. I’d recommend the customer leave it in for now, so he/she can use it for some basic testing. For actual experiments, you replace mutest plastic with the sample you want to check. Connect the permeation cell as shown above, using VCR gaskets (included), and connect the far end to the multi-temperature vacuum hose, provided. Do this outside of the chamber first, as a preliminary test to see if everything is working.

For a first test live the connections to the high pressure top section unconnected. The pressure then will be 1 atm, and the chamber will be full of air. eave the top, Connect the power to the vacuum pressure gauge reader and connect the gauge reader to the gauge head. Open the valve and turn on the pump. If there are no leaks the pressure should fall precipitously, and you should see little to no vapor coming out the out port on the vacuum pump. If there is vapor, you’ve got a leak, and you should find it; perhaps you didn’t tighten a VCR connection, or you didn’t do a good job with the vacuum hose. When things are going well, you should see the pressure drop to the single-digit, milliTorr range. If you close the valve, you’ll see the pressure rise in the gauge. This is mostly water and air degassing from the plastic sample. After 30 minutes, the rate of degassing should slow and you should be able to measure the rate of gas permeation in the polymer. With my test plastic, it took a minute or so for the pressure to rise by 10 milliTorr after I closed the valve.

If you like, you can now repeat this preliminary experiment with hydrogen connect the hydrogen line to one of the two ports on the top of the permeation cell and connect the other port to the rest of the copper tubing. Attach the H2 bleed restrictor (provided) at the end of this tubing. Now turn on the H2 pressure to some reasonable value — 45 psig, say. With 45 psi (3 barg upstream) you will have a ∆P of 60 psia or 4 atm across the membrane; vacuum equals -15 psig. Repeat the experiment above; pump everything down, close the valve and note that the pressure rises faster. The restrictor allows you to maintain a H2 pressure with a small, cleansing flow of gas through the cell.

If you like to do these experiments with a computer record, this might be a good time to connect your computer to the vacuum reader/ controller, and to the thermocouple, and to the N2 pressure sensor. 

Here’s how I calculate the permeability of the test polymer from the time it takes for a pressure rise assuming air as the permeating gas. The volume of the vacuumed out area after the valve is 32 cc; there is an open area in the cell of 13.0 cm2 and, as it happens, the  thickness of the test plastic is 2 mm. To calculate the permeation rate, measure the time to rise 10 millitorr. Next calculate the millitorr per hour: that’s 360 divided by the time to rise ten milliTorr. To calculate ncc/day, multiply the millitorr/hour by 24 and by the volume of the chamber, 32 cc, and divide by 760,000, the number of milliTorr in an atmosphere. I found that, for air permeation at ∆P = one atm, I was getting 1 minute per milliTorr, which translates to about 0.5 ncc/day of permeation through my test polymer sheet. To find the specific permeability in cc.mm/m2.day.atm, I multiply this last number by the thickness of the plastic (2 mm in this case), divide by the area, 0.0013 m2, and divide by ∆P, 1 atm, for this first test. Calculated this way, I got an air permeance of 771 cc.mm/m2.day.atm.

The complete setup for permeation testing.

The complete setup for permeation testing.

Now repeat the experiment with hydrogen and your own plastic. Disconnect the cell from both the vacuum line and from the hydrogen in line. Open the cell; take out my test plastic and replace it with your own sample, 1.87” diameter, or so. Replace the gasket, or reuse it. Center the top on the bottom and retighten the bolts. I used 25 Nt-m of torque, but part of that was using a very soft rubbery plastic. You might want to use a little more — perhaps 40-50 Nt-m. Seal everything up. Check that it is leak tight, and you are good to go.

The experimental method is the same as before and the only signficant change when working with hydrogen, besides the need for a nitrogen flush, is that you should multiply the time to reach 10 milliTorr by the square-root of seven, 2.646. Alternatively, you can multiply the calculated permeability by 0.378. The pressure sensor provided measures heat transfer and hydrogen is a better heat transfer material than nitrogen by a factor of √7. The vacuum gauge is thus more sensitive to H2 than to N2. When the gauge says that a pressure change of 10 milliTorr has occurred, in actuality, it’s only 3.78 milliTorr.  The pressure gauge reads 3.78 milliTorr oh hydrogen as 10 milliTorr.

You can speed experiments by a factor of ten, by testing the time to rise 1 millitorr instead of ten. At these low pressures, the gauge I provided reads in hundredths of a milliTorr. Alternately, for higher permeation plastics (or metals) you want to test the time to rise 100 milliTorr or more, otherwise the experiment is over too fast. Even at a ten millTorr change, this device gives good accuracy in under 1 hour with even the most permeation-resistant polymers.

Dr. Robert E. Buxbaum, March 27, 2019; If you’d like one of these, just ask. Here’s a link to our web site, REB Research,

Of God and gauge blocks

Leave a reply

Most scientists are religious on some level. There’s clear evidence for a big bang, and thus for a God-of-Creation. But the creation event is so distant and huge that no personal God is implied. I’d like to suggest that the God of creation is close by and as a beginning to this, I’d like to discus Johansson gauge blocks, the standard tool used to measure machine parts accurately.

jo4

A pair of Johansson blocks supporting 100 kg in a 1917 demonstration. This is 33 times atmospheric pressure, about 470 psi.

Lets say you’re making a complicated piece of commercial machinery, a car engine for example. Generally you’ll need to make many parts in several different shops using several different machines. If you want to be sure the parts will fit together, a representative number of each part must be checked for dimensional accuracy in several places. An accuracy requirement of 0.01 mm is not uncommon. How would you do this? The way it’s been done, at least since the days of Henry Ford, is to mount the parts to a flat surface and use a feeler gauge to compare the heights of the parts to the height of stacks of precisely manufactured gauge blocks. Called Johansson gauge blocks after the inventor and original manufacturer, Henrik Johansson, the blocks are typically made of steel, 1.35″ wide by .35″ thick (0.47 in2 surface), and of various heights. Different height blocks can be stacked to produce any desired height in multiples of 0.01 mm. To give accuracy to the measurements, the blocks must be manufactured flat to within 1/10000 of a millimeter. This is 0.1µ, or about 1/5 the wavelength of visible light. At this degree of flatness an amazing thing is seen to happen: Jo blocks stick together when stacked with a force of 100 kg (220 pounds) or more, an effect called, “wringing.” See picture at right from a 1917 advertising demonstration.

This 220 lbs of force measured in the picture suggests an invisible pressure of 470 psi at least that holds the blocks together (220 lbs/0.47 in2 = 470 psi). This is 32 times the pressure of the atmosphere. It is independent of air, or temperature, or the metal used to make the blocks. Since pressure times volume equals energy, and this pressure can be thought of as a vacuum energy density arising “out of the nothingness.” We find that each cubic foot of space between the blocks contains, 470 foot-lbs of energy. This is the equivalent of 0.9 kWh per cubic meter, energy you can not see, but you can feel. That is a lot of energy in the nothingness, but the energy (and the pressure) get larger the flatter you make the surfaces, or the closer together you bring them together. This is an odd observation since, generally get more dense the smaller you divide them. Clean metal surfaces that are flat enough will weld together without the need for heat, a trick we have used in the manufacture of purifiers.

A standard way to think of quantum scattering is that the particle is scattered by invisible bits of light (virtual photons), the wavy lines. In this view, the force that pushes two flat surfaces together is from a slight deficiency in the amount of invisible light in the small space between them.

A standard way to think of quantum scattering of an atom (solid line) is that it is scattered by invisible bits of light, virtual photons (the wavy lines). In this view, the force that pushes two blocks together comes from a slight deficiency in the number of virtual photons in the small space between the blocks.

The empty space between two flat surfaces also has the power to scatter light or atoms that pass between them. This scattering is seen even in vacuum at zero degrees Kelvin, absolute zero. Somehow the light or atoms picks up energy, “out of the nothingness,” and shoots up or down. It’s a “quantum effect,” and after a while physics students forget how odd it is for energy to come out of nothing. Not only do students stop wondering about where the energy comes from, they stop wondering why it is that the scattering energy gets bigger the closer you bring the surfaces. With Johansson block sticking and with quantum scattering, the energy density gets higher the closer the surface, and this is accepted as normal, just Heisenberg’s uncertainly in two contexts. You can calculate the force from the zero-point energy of vacuum, but you must add a relativistic wrinkle: the distance between two surfaces shrinks the faster you move according to relativity, but measurable force should not. A calculation of the force that includes both quantum mechanics and relativity was derived by Hendrik Casimir:

Energy per volume = P = F/A = πhc/ 480 L4,

where P is pressure, F is force, A is area, h is plank’s quantum constant, 6.63×10−34 Js, c is the speed of light, 3×108 m/s, and L is the distance between the plates, m. Experiments have been found to match the above prediction to within 2%, experimental error, but the energy density this implies is huge, especially when L is small, the equation must apply down to plank lengths, 1.6×10-35 m. Even at the size of an atom, 1×10-10m, the amount of the energy you can see is 3.6 GWhr/m3, 3.6 Giga Watts. 3.6 GigaWatt hrs is one hour’s energy output of three to four large nuclear plants. We see only a tiny portion of the Plank-length vacuum energy when we stick Johansson gauge blocks together, but the rest is there, near invisible, in every bit of empty space. The implication of this enormous energy remains baffling in any analysis. I see it as an indication that God is everywhere, exceedingly powerful, filling the universe, and holding everything together. Take a look, and come to your own conclusions.

As a homiletic, it seems to me that God likes friendship, but does not desire shaman, folks to stand between man and Him. Why do I say that? The huge force-energy between plates brings them together, but scatters anything that goes between. And now you know something about nothing.

Robert Buxbaum, November 7, 2018. Physics references: H. B. G. Casimir and D. Polder. The Influence of Retardation on the London-van der Waals Forces. Phys. Rev. 73, 360 (1948).
S. Lamoreaux, Phys. Rev. Lett. 78, 5 (1996).

Isotopic effects in hydrogen diffusion in metals

1 Reply

For most people, there is a fundamental difference between solids and fluids. Solids have long-term permanence with no apparent diffusion; liquids diffuse and lack permanence. Put a penny on top of a dime, and 20 years later the two coins are as distinct as ever. Put a layer of colored water on top of plain water, and within a few minutes you’ll see that the coloring diffuse into the plain water, or (if you think the other way) you’ll see the plain water diffuse into the colored.

Now consider the transport of hydrogen in metals, the technology behind REB Research’s metallic  membranes and getters. The metals are clearly solid, keeping their shapes and properties for centuries. Still, hydrogen flows into and through the metals at a rate of a light breeze, about 40 cm/minute. Another way of saying this is we transfer 30 to 50 cc/min of hydrogen through each cm2 of membrane at 200 psi and 400°C; divide the volume by the area, and you’ll see that the hydrogen really moves through the metal at a nice clip. It’s like a normal filter, but it’s 100% selective to hydrogen. No other gas goes through.

To explain why hydrogen passes through the solid metal membrane this way, we have to start talking about quantum behavior. It was the quantum behavior of hydrogen that first interested me in hydrogen, some 42 years ago. I used it to explain why water was wet. Below, you will find something a bit more mathematical, a quantum explanation of hydrogen motion in metals. At REB we recently put these ideas towards building a membrane system for concentration of heavy hydrogen isotopes. If you like what follows, you might want to look up my thesis. This is from my 3rd appendix.

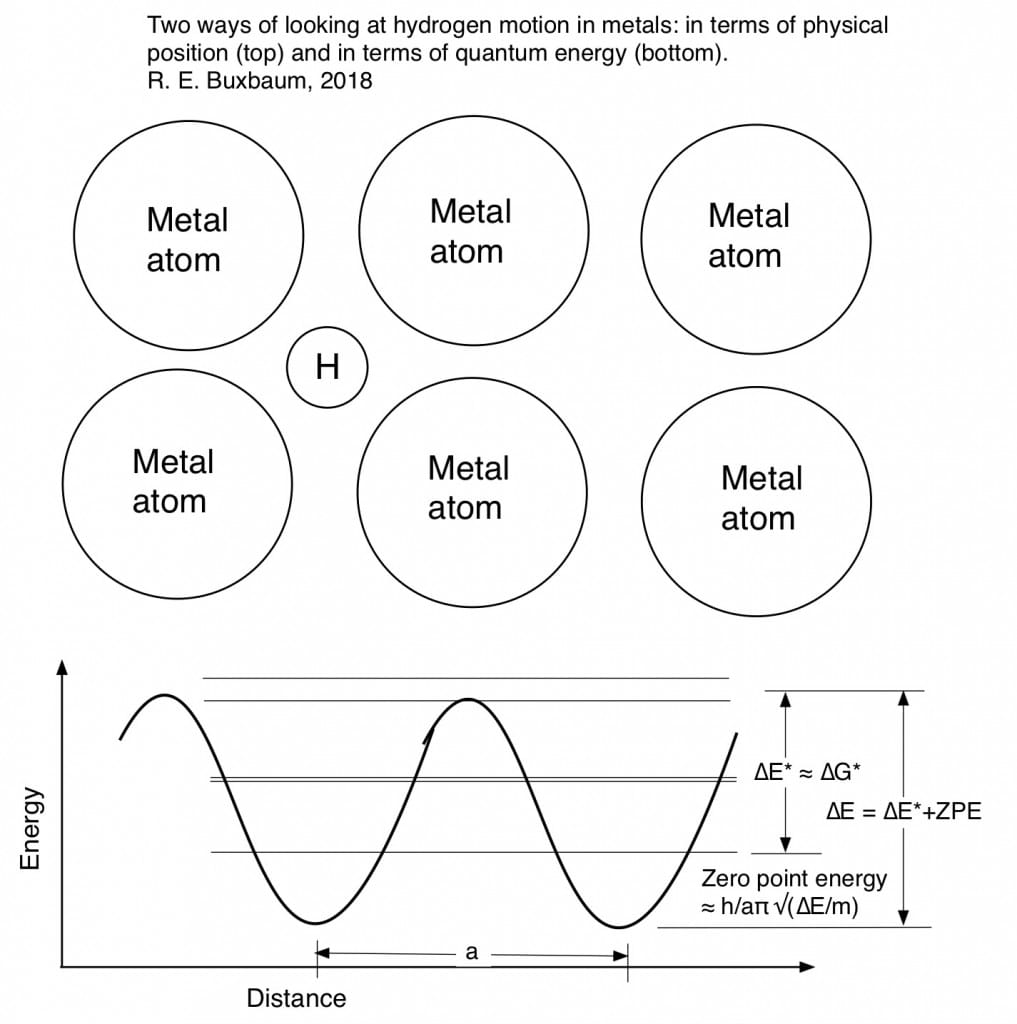
Although no-one quite understands why nature should work this way, it seems that nature works by quantum mechanics (and entropy). The basic idea of quantum mechanics you will know that confined atoms can only occupy specific, quantized energy levels as shown below. The energy difference between the lowest energy state and the next level is typically high. Thus, most of the hydrogen atoms in an atom will occupy only the lower state, the so-called zero-point-energy state.

A hydrogen atom, shown occupying an interstitial position between metal atoms (above), is also occupying quantum states (below). The lowest state, ZPE is above the bottom of the well. Higher energy states are degenerate: they appear in pairs. The rate of diffusive motion is related to ∆E* and this degeneracy.

A hydrogen atom, shown occupying an interstitial position between metal atoms (above), is also occupying quantum states (below). The lowest state, ZPE is above the bottom of the well. Higher energy states are degenerate: they appear in pairs. The rate of diffusive motion is related to ∆E* and this degeneracy.

The fraction occupying a higher energy state is calculated as c*/c = exp (-∆E*/RT). where ∆E* is the molar energy difference between the higher energy state and the ground state, R is the gas constant and T is temperature. When thinking about diffusion it is worthwhile to note that this energy is likely temperature dependent. Thus ∆E* = ∆G* = ∆H* – T∆S* where asterisk indicates the key energy level where diffusion takes place — the activated state. If ∆E* is mostly elastic strain energy, we can assume that ∆S* is related to the temperature dependence of the elastic strain.

Thus,

∆S* = -∆E*/Y dY/dT

where Y is the Young’s modulus of elasticity of the metal. For hydrogen diffusion in metals, I find that ∆S* is typically small, while it is often typically significant for the diffusion of other atoms: carbon, nitrogen, oxygen, sulfur…

The rate of diffusion is now calculated assuming a three-dimensional drunkards walk where the step lengths are constant = a. Rayleigh showed that, for a simple cubic lattice, this becomes:

D = a2/6τ

a is the distance between interstitial sites and t is the average time for crossing. For hydrogen in a BCC metal like niobium or iron, D=

a2/9τ; for a FCC metal, like palladium or copper, it’s

a2/3τ. A nice way to think about τ, is to note that it is only at high-energy can a hydrogen atom cross from one interstitial site to another, and as we noted most hydrogen atoms will be at lower energies. Thus,

τ = ω c*/c = ω exp (-∆E*/RT)

where ω is the approach frequency, or the amount of time it takes to go from the left interstitial position to the right one. When I was doing my PhD (and still likely today) the standard approach of physics writers was to use a classical formulation for this time-scale based on the average speed of the interstitial. Thus, ω = 1/2a√(kT/m), and

τ = 1/2a√(kT/m) exp (-∆E*/RT).

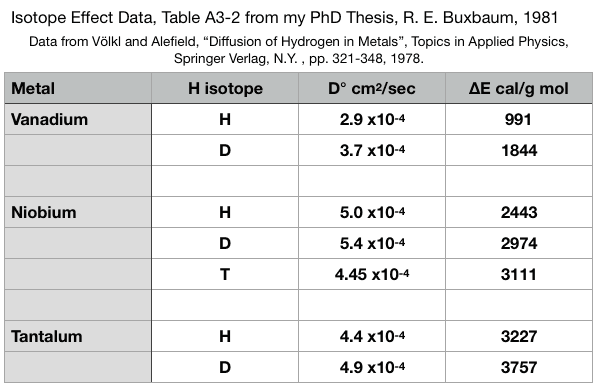
In the above, m is the mass of the hydrogen atom, 1.66 x 10-24 g for protium, and twice that for deuterium, etc., a is the distance between interstitial sites, measured in cm, T is temperature, Kelvin, and k is the Boltzmann constant, 1.38 x 10-16 erg/°K. This formulation correctly predicts that heavier isotopes will diffuse slower than light isotopes, but it predicts incorrectly that, at all temperatures, the diffusivity of deuterium is 1/√2 that for protium, and that the diffusivity of tritium is 1/√3 that of protium. It also suggests that the activation energy of diffusion will not depend on isotope mass. I noticed that neither of these predictions is borne out by experiment, and came to wonder if it would not be more correct to assume ω represent the motion of the lattice, breathing, and not the motion of a highly activated hydrogen atom breaking through an immobile lattice. This thought is borne out by experimental diffusion data where you describe hydrogen diffusion as D = D° exp (-∆E*/RT).

Screen Shot 2018-06-21 at 12.08.20 AM

You’ll notice from the above that D° hardly changes with isotope mass, in complete contradiction to the above classical model. Also note that ∆E* is very isotope dependent. This too is in contradiction to the classical formulation above. Further, to the extent that D° does change with isotope mass, D° gets larger for heavier mass hydrogen isotopes. I assume that small difference is the entropy effect of ∆E* mentioned above. There is no simple square-root of mass behavior in contrast to most of the books we had in grad school.

As for why ∆E* varies with isotope mass, I found that I could get a decent explanation of my observations if I assumed that the isotope dependence arose from the zero point energy. Heavier isotopes of hydrogen will have lower zero-point energies, and thus ∆E* will be higher for heavier isotopes of hydrogen. This seems like a far better approach than the semi-classical one, where ∆E* is isotope independent.

I will now go a bit further than I did in my PhD thesis. I’ll make the general assumption that the energy well is sinusoidal, or rather that it consists of two parabolas one opposite the other. The ZPE is easily calculated for parabolic energy surfaces (harmonic oscillators). I find that ZPE = h/aπ √(∆E/m) where m is the mass of the particular hydrogen atom, h is Plank’s constant, 6.63 x 10-27 erg-sec,  and ∆E is ∆E* + ZPE, the zero point energy. For my PhD thesis, I didn’t think to calculate ZPE and thus the isotope effect on the activation energy. I now see how I could have done it relatively easily e.g. by trial and error, and a quick estimate shows it would have worked nicely. Instead, for my PhD, Appendix 3, I only looked at D°, and found that the values of D° were consistent with the idea that ω is about 0.55 times the Debye frequency, ω ≈ .55 ωD. The slight tendency for D° to be larger for heavier isotopes was explained by the temperature dependence of the metal’s elasticity.

Two more comments based on the diagram I presented above. First, notice that there is middle split level of energies. This was an explanation I’d put forward for quantum tunneling atomic migration that some people had seen at energies below the activation energy. I don’t know if this observation was a reality or an optical illusion, but present I the energy picture so that you’ll have the beginnings of a description. The other thing I’d like to address is the question you may have had — why is there no zero-energy effect at the activated energy state. Such a zero energy difference would cancel the one at the ground state and leave you with no isotope effect on activation energy. The simple answer is that all the data showing the isotope effect on activation energy, table A3-2, was for BCC metals. BCC metals have an activation energy barrier, but it is not caused by physical squeezing between atoms, as for a FCC metal, but by a lack of electrons. In a BCC metal there is no physical squeezing, at the activated state so you’d expect to have no ZPE there. This is not be the case for FCC metals, like palladium, copper, or most stainless steels. For these metals there is a much smaller, on non-existent isotope effect on ∆E*.

Robert Buxbaum, June 21, 2018. I should probably try to answer the original question about solids and fluids, too: why solids appear solid, and fluids not. My answer has to do with quantum mechanics: Energies are quantized, and always have a ∆E* for motion. Solid materials are those where ω exp (-∆E*/RT) has unit of centuries. Thus, our ability to understand the world is based on the least understandable bit of physics.

Survey on hydrogen use

Leave a reply

My company makes hydrogen generators: devices that make ultra-pure hydrogen on demand from methanol and water using a membrane reactor. If you use hydrogen, please fill out the following survey. I need to know my customers needs better, e.g. so that I will know if I should add a compressor. Thanks.

Create your own user feedback survey

Robert Buxbaum, June 13, 2018