Category Archives: math

The Scientific Method isn’t the method of scientists

13 Replies

A linchpin of middle school and high-school education is teaching ‘the scientific method.’ This is the method, students are led to believe, that scientists use to determine Truths, facts, and laws of nature. Scientists, students are told, start with a hypothesis of how things work or should work, they then devise a set of predictions based on deductive reasoning from these hypotheses, and perform some critical experiments to test the hypothesis and determine if it is true (experimentum crucis in Latin). Sorry to say, this is a path to error, and not the method that scientists use. The real method involves a few more steps, and follows a different order and path. It instead follows the path that Sherlock Holmes uses to crack a case.

The actual method of Holmes, and of science, is to avoid beginning with a hypothesis. Isaac Newton claimed: “I never make hypotheses” Instead as best we can tell, Newton, like most scientists, first gathered as much experimental evidence on a subject as possible before trying to concoct any explanation. As Holmes says (Study in Scarlet): “It is a capital mistake to theorize before you have all the evidence. It biases the judgment.”

It is a capital mistake to theorize before one has data. Insensibly one begins to twist facts to suit theories, instead of theories to suit facts (Holmes, Scandal in Bohemia).

Holmes barely tolerates those who hypothesize before they have all the data: “It is a capital mistake to theorize before one has data. Insensibly one begins to twist facts to suit theories, instead of theories to suit facts.” (Scandal in Bohemia).

Then there is the goal of science. It is not the goal of science to confirm some theory, model, or hypothesis; every theory probably has some limited area where it’s true. The goal for any real-life scientific investigation is the desire to explain something specific and out of the ordinary, or do something cool. Similarly, with Sherlock Holmes, the start of the investigation is the arrival of a client with a specific, unusual need – one that seems a bit outside of the normal routine. Similarly, the scientist wants to do something: build a bigger bridge, understand global warming, or how DNA directs genetics; make better gunpowder, cure a disease, or Rule the World (mad scientists favor this). Once there is a fixed goal, it is the goal that should direct the next steps: it directs the collection of data, and focuses the mind on the wide variety of types of solution. As Holmes says: , “it’s wise to make one’s self aware of the potential existence of multiple hypotheses, so that one eventually may choose one that fits most or all of the facts as they become known.” It’s only when there is no goal, that any path will do. 

In gathering experimental data (evidence), most scientists spend months in the less-fashionable sections of the library, looking at the experimental methods and observations of others, generally from many countries, collecting any scrap that seems reasonably related to the goal at hand. I used 3 x5″ cards to catalog this data and the references. From many books and articles, one extracts enough diversity of data to be able to look for patterns and to begin to apply inductive logic. “The little things are infinitely the most important” (Case of Identity). You have to look for patterns in the data you collect. Holmes does not explain how he looks for patterns, but this skill is innate in most people to a greater or lesser extent. A nice set approach to inductive logic is called the Baconian Method, it would be nice to see schools teach it. If the author is still alive, a scientist will try to contact him or her to clarify things. In every SH mystery, Holmes does the same and is always rewarded. There is always some key fact or observation that this turns up: key information unknown to the original client.

Based on the facts collected one begins to create the framework for a variety of mathematical models: mathematics is always involved, but these models should be pretty flexible. Often the result is a tree of related, mathematical models, each highlighting some different issue, process, or problem. One then may begin to prune the tree, trying to fit the known data (facts and numbers collected), into a mathematical picture of relevant parts of this tree. There usually won’t be quite enough for a full picture, but a fair amount of progress can usually be had with the application of statistics, calculus, physics, and chemistry. These are the key skills one learns in college, but usually the high-schooler and middle schooler has not learned them very well at all. If they’ve learned math and physics, they’ve not learned it in a way to apply it to something new, quite yet (it helps to read the accounts of real scientists here — e.g. The Double Helix by J. Watson).

Usually one tries to do some experiments at this stage. Homes might visit a ship or test a poison, and a scientist might go off to his, equally-smelly laboratory. The experiments done there are rarely experimenti crucae where one can say they’ve determined the truth of a single hypothesis. Rather one wants to eliminated some hypotheses and collect data to be used to evaluate others. An answer generally requires that you have both a numerical expectation and that you’ve eliminated all reasonable explanations but one. As Holmes says often, e.g. Sign of the four, “when you have excluded the impossible, whatever remains, however improbable, must be the truth”. The middle part of a scientific investigation generally involves these practical experiments to prune the tree of possibilities and determine the coefficients of relevant terms in the mathematical model: the weight or capacity of a bridge of a certain design, the likely effect of CO2 on global temperature, the dose response of a drug, or the temperature and burn rate of different gunpowder mixes. Though not mentioned by Holmes, it is critically important in science to aim for observations that have numbers attached.

The destruction of false aspects and models is a very important part of any study. Francis Bacon calls this act destruction of idols of the mind, and it includes many parts: destroying commonly held presuppositions, avoiding personal preferences, avoiding the tendency to see a closer relationship than can be justified, etc.

In science, one eliminates the impossible through the use of numbers and math, generally based on your laboratory observations. When you attempt to the numbers associated with our observations to the various possible models some will take the data well, some poorly; and some twill not fit the data at all. Apply the deductive reasoning that is taught in schools: logical, Boolean, step by step; if some aspect of a model does not fit, it is likely the model is wrong. If we have shown that all men are mortal, and we are comfortable that Socrates is a man, then it is far better to conclude that Socrates is mortal than to conclude that all men but Socrates is mortal (Occam’s razor). This is the sort of reasoning that computers are really good at (better than humans, actually). It all rests on the inductive pattern searches similarities and differences — that we started with, and very often we find we are missing a piece, e.g. we still need to determine that all men are indeed mortal, or that Socrates is a man. It’s back to the lab; this is why PhDs often take 5-6 years, and not the 3-4 that one hopes for at the start.

More often than not we find we have a theory or two (or three), but not quite all the pieces in place to get to our goal (whatever that was), but at least there’s a clearer path, and often more than one. Since science is goal oriented, we’re likely to find a more efficient than we fist thought. E.g. instead of proving that all men are mortal, show it to be true of Greek men, that is for all two-legged, fairly hairless beings who speak Greek. All we must show is that few Greeks live beyond 130 years, and that Socrates is one of them.

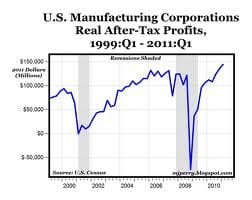
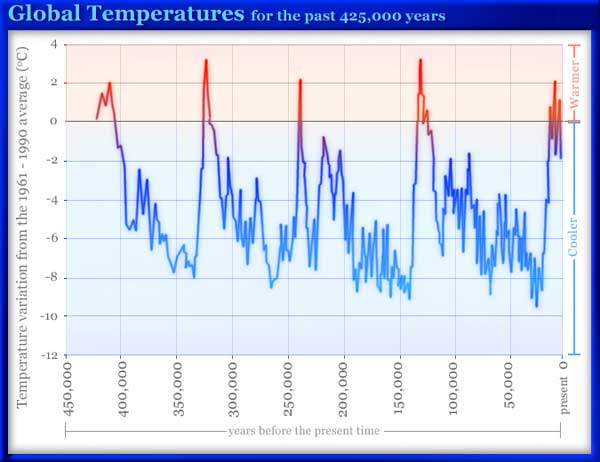
Putting numerical values on the mathematical relationship is a critical step in all science, as is the use of models — mathematical and otherwise. The path to measure the life expectancy of Greeks will generally involve looking at a sample population. A scientist calls this a model. He will analyze this model using statistical model of average and standard deviation and will derive his or her conclusions from there. It is only now that you have a hypothesis, but it’s still based on a model. In health experiments the model is typically a sample of animals (experiments on people are often illegal and take too long). For bridge experiments one uses small wood or metal models; and for chemical experiments, one uses small samples. Numbers and ratios are the key to making these models relevant in the real world. A hypothesis of this sort, backed by numbers is publishable, and is as far as you can go when dealing with the past (e.g. why Germany lost WW2, or why the dinosaurs died off) but the gold-standard of science is predictability.  Thus, while we a confident that Socrates is definitely mortal, we’re not 100% certain that global warming is real — in fact, it seems to have stopped though CO2 levels are rising. To be 100% sure you’re right about global warming we have to make predictions, e.g. that the temperature will have risen 7 degrees in the last 14 years (it has not), or Al Gore’s prediction that the sea will rise 8 meters by 2106 (this seems unlikely at the current time). This is not to blame the scientists whose predictions don’t pan out, “We balance probabilities and choose the most likely. It is the scientific use of the imagination” (Hound of the Baskervilles). The hope is that everything matches; but sometimes we must look for an alternative; that’s happened rarely in my research, but it’s happened.

You are now at the conclusion of the scientific process. In fiction, this is where the criminal is led away in chains (or not, as with “The Woman,” “The Adventure of the Yellow Face,” or of “The Blue Carbuncle” where Holmes lets the criminal free — “It’s Christmas”). For most research the conclusion includes writing a good research paper “Nothing clears up a case so much as stating it to another person”(Memoirs). For a PhD, this is followed by the search for a good job. For a commercial researcher, it’s a new product or product improvement. For the mad scientist, that conclusion is the goal: taking over the world and enslaving the population (or not; typically the scientist is thwarted by some detail!). But for the professor or professional research scientist, the goal is never quite reached; it’s a stepping stone to a grant application to do further work, and from there to tenure. In the case of the Socrates mortality work, the scientist might ask for money to go from country to country, measuring life-spans to demonstrate that all philosophers are mortal. This isn’t as pointless and self-serving as it seems, Follow-up work is easier than the first work since you’ve already got half of it done, and you sometimes find something interesting, e.g. about diet and life-span, or diseases, etc. I did some 70 papers when I was a professor, some on diet and lifespan.

One should avoid making some horrible bad logical conclusion at the end, by the way. It always seems to happen that the mad scientist is thwarted at the end; the greatest criminal masterminds are tripped by some last-minute flaw. Similarly the scientist must not make that last-mistep. “One should always look for a possible alternative, and provide against it” (Adventure of Black Peter). Just because you’ve demonstrated that  iodine kills germs, and you know that germs cause disease, please don’t conclude that drinking iodine will cure your disease. That’s the sort of science mistakes that were common in the middle ages, and show up far too often today. In the last steps, as in the first, follow the inductive and quantitative methods of Paracelsus to the end: look for numbers, (not a Holmes quote) check how quantity and location affects things. In the case of antiseptics, Paracelsus noticed that only external cleaning helped and that the help was dose sensitive.

As an example in the 20th century, don’t just conclude that, because bullets kill, removing the bullets is a good idea. It is likely that the trauma and infection of removing the bullet is what killed Lincoln, Garfield, and McKinley. Theodore Roosevelt was shot too, but decided to leave his bullet where it was, noticing that many shot animals and soldiers lived for years with bullets in them; and Roosevelt lived for 8 more years. Don’t make these last-minute missteps: though it’s logical to think that removing guns will reduce crime, the evidence does not support that. Don’t let a leap of bad deduction at the end ruin a line of good science. “A few flies make the ointment rancid,” said Solomon. Here’s how to do statistics on data that’s taken randomly.

Dr. Robert E. Buxbaum, scientist and Holmes fan wrote this, Sept 2, 2013. My thanks to Lou Manzione, a friend from college and grad school, who suggested I reread all of Holmes early in my PhD work, and to Wikiquote, a wonderful site where I found the Holmes quotes; the Solomon quote I knew, and the others I made up.

Slowing Cancer with Fish and Unhealth Food

7 Replies

Some 25 years ago, while still a chemical engineering professor at Michigan State University, I did some statistical work for a group in the Physiology department on the relationship between diet and cancer. The research involved giving cancer to groups of rats and feeding them different diets of the same calorie intake to see which promoted or slowed the disease. It had been determined that low-calorie diets slowed cancer growth, and were good for longevity in general, while overweight rats died young (true in humans too, by the way, though there’s a limit and starvation will kill you).

The group found that fish oil was generally good for you, but they found that there were several unhealthy foods that slowed cancer growth in rats. The statistics were clouded by the fact that cancer growth rates are not normally distributed, and I was brought in to help untangle the observations.

With help from probability paper (a favorite trick of mine), I confirmed that healthy rats fared better on healthily diets, but cancerous rats did better with some unhealth food. Sick or well, all rats did best with fish oil, and all rats did pretty well with olive oil, but the cancerous rats did better with lard or palm oil (normally an unhealthy diet) and very poorly with corn oil or canola, oils that are normally healthful. The results are published in several articles in the journals “Cancer” and “Cancer Research.”

Among vitamins, they found something similar (it was before I joined the group). Several anti-oxidizing vitamins, A, D and E made things worse for carcinogenic rats while being good for healthy rats (and for people in moderation). Moderation is key; too much of a good thing isn’t good, and a diet with too much fish oil promotes cancer.

What seems to be happening is that the cancer cells grow at the same rate with all of the equi-caloric diets, but that there was a difference the rate of natural cancer cell death. More cancer cells died when the rat was fed junk food oils than those fed a diet of corn oil and canola. Similarly, the reason anti-oxidizing vitamins hurt cancerous rats was that fewer cancer cells died when the rats were fed these vitamins. A working hypothesis is that the junk oils (and the fish oil) produced free radicals that did more damage to the cancer than to the rats. In healthy rats (and people), these free radicals are bad, promoting cell mutation, cell degradation, and sometimes cancer. But perhaps our body use these same free radicals to fight disease.

Larger amounts of vitamins A, D, and E hurt cancerous-rats by removing the free radicals they normally use fight the disease, or so our model went. Bad oils and fish-oil in moderation, with calorie intake held constant, helped slow the cancer, by a presumed mechanism of adding a few more free radicals. Fish oil, it can be assumed, killed some healthy cells in the healthy rats too, but not enough to cause problems when taken in moderation. Even healthy people are often benefitted by poisons like sunlight, coffee, alcohol and radiation.

At this point, a warning is in-order: Don’t rely on fish oil and lard as home remedies if you’ve got cancer. Rats are not people, and your calorie intake is not held artificially constant with no other treatments given. Get treated by a real doctor — he or she will use radiation and/ or real drugs, and those will form the right amount of free radicals, targeted to the right places. Our rats were given massive amounts of cancer and had no other treatment besides diet. Excess vitamin A has been shown to be bad for humans under treatment for lung cancer, and that’s perhaps because of the mechanism we imagine, or perhaps everything works by some other mechanism. However it works, a little fish in your diet is probably a good idea whether you are sick or well.

A simpler health trick is that it couldn’t hurt most Americans is a lower calorie diet, especially if combined with exercise. Dr. Mites, a colleague of mine in the department (now deceased at 90+) liked to say that, if exercise could be put into a pill, it would be the most prescribed drug in America. There are few things that would benefit most Americans more than (moderate) exercise. There was a sign in the physiology office, perhaps his doing, “If it’s physical, it’s therapy.”

Anyway these are some useful things I learned as an associate professor in the physiology department at Michigan State. I ended up writing 30-35 physiology papers, e.g. on how cells crawl and cell regulation through architecture; and I met a lot of cool people. Perhaps I’ll blog more about health, biology, the body, or about non-normal statistics and probability paper. Please tell me what you’re interested in, or give me some keen insights of your own.

Dr. Robert Buxbaum is a Chemical Engineer who mostly works in hydrogen I’ve published some 75 technical papers, including two each in Science and Nature: fancy magazines that you’d normally have to pay for, but this blog is free. August 14, 2013

Control engineer joke

6 Replies

What made the control engineer go crazy?

 

He got positive feedback.

Is funny because …… it’s a double entente, where both meanings are true: (1) control engineers very rarely get compliments (positive feedback); the aim of control is perfection, something that’s unachievable for a dynamic system (and generally similar to near perfection: the slope at a maximum is zero). Also (2) systems go unstable if the control feedback is positive. This can happen if the controller was set backwards, but more usually happens when the response is too fast or too extreme. Positive feedback pushes a system further to error and the process either blows up, or (more commonly) goes wildly chaotic, oscillating between two or more “strange attractor” states.

It seems to me that hypnosis, control-freak love, and cult behaviors are the result of intentionally produced positive feedback. Palsies, economic cycles, and global warming are more likely the result of unintentional positive feedback. In each case, the behavior is oscillatory chaotic.

The normal state of Engineering is lack of feedback. Perhaps this is good because messed up feedback leads to worse results. From xykd.

Our brains give little reliable feedback on how well they work, but that may be better than strong, immediate feedback, as that could lead to bipolar instability. From xkcd. For more on this idea, see Science and Sanity, by Alfred Korzbski (mini youtube)

Control engineers tend to be male (85%), married (80%), happy people (at least they claim to be happy). Perhaps they know that near-perfection is close enough for a complex system in a dynamic world, or that one is about as happy as believes ones-self to be. It also helps that control engineer salaries are about $95,000/ year with excellent benefits and low employment turnover.

Here’s a chemical engineer joke I made up, and an older engineering joke. If you like, I’ll be happy to consult with you on the behavior of your processes.

By Dr. Robert E. Buxbaum, July 4, 2013

Another Quantum Joke, and Schrödinger’s waves derived

4 Replies
Quantum mechanics joke. from xkcd.

Quantum mechanics joke. from xkcd.

Is funny because … it’s is a double entente on the words grain (as in grainy) and waves, as in Schrödinger waves or “amber waves of grain” in the song America (Oh Beautiful). In Schrödinger’s view of the quantum world everything seems to exist or move as a wave until you observe it, and then it always becomes a particle. The math to solve for the energy of things is simple, and thus the equation is useful, but it’s hard to understand why,  e.g. when you solve for the behavior of a particle (atom) in a double slit experiment you have to imagine that the particle behaves as an insubstantial wave traveling though both slits until it’s observed. And only then behaves as a completely solid particle.

Math equations can always be rewritten, though, and science works in the language of math. The different forms appear to have different meaning but they don’t since they have the same practical predictions. Because of this freedom of meaning (and some other things) science is the opposite of religion. Other mathematical formalisms for quantum mechanics may be more comforting, or less, but most avoid the wave-particle duality.

The first formalism was Heisenberg’s uncertainty. At the end of this post, I show that it is identical mathematically to Schrödinger’s wave view. Heisenberg’s version showed up in two quantum jokes that I explained (beat into the ground), one about a lightbulb  and one about Heisenberg in a car (also explains why water is wet or why hydrogen diffuses through metals so quickly).

Yet another quantum formalism involves Feynman’s little diagrams. One assumes that matter follows every possible path (the multiple universe view) and that time should go backwards. As a result, we expect that antimatter apples should fall up. Experiments are underway at CERN to test if they do fall up, and by next year we should finally know if they do. Even if anti-apples don’t fall up, that won’t mean this formalism is wrong, BTW: all identical math forms are identical, and we don’t understand gravity well in any of them.

Yet another identical formalism (my favorite) involves imagining that matter has a real and an imaginary part. In this formalism, the components move independently by diffusion, and as a result look like waves: exp (-it) = cost t + i sin t. You can’t observe the two parts independently though, only the following product of the real and imaginary part: (the real + imaginary part) x (the real – imaginary part). Slightly different math, same results, different ways of thinking of things.

Because of quantum mechanics, hydrogen diffuses very quickly in metals: in some metals quicker than most anything in water. This is the basis of REB Research metal membrane hydrogen purifiers and also causes hydrogen embrittlement (explained, perhaps in some later post). All other elements go through metals much slower than hydrogen allowing us to make hydrogen purifiers that are effectively 100% selective. Our membranes also separate different hydrogen isotopes from each other by quantum effects (big things tunnel slower). Among the uses for our hydrogen filters is for gas chromatography, dynamo cooling, and to reduce the likelihood of nuclear accidents.

Dr. Robert E. Buxbaum, June 18, 2013.

To see Schrödinger’s wave equation derived from Heisenberg for non-changing (time independent) items, go here and note that, for a standing wave there is a vibration in time, though no net change. Start with a version of Heisenberg uncertainty: h =  λp where the uncertainty in length = wavelength = λ and the uncertainty in momentum = momentum = p. The kinetic energy, KE = 1/2 p2/m, and KE+U(x) =E where E is the total energy of the particle or atom, and U(x) is the potential energy, some function of position only. Thus, p = √2m(E-PE). Assume that the particle can be described by a standing wave with a physical description, ψ, and an imaginary vibration you can’t ever see, exp(-iωt). And assume this time and space are completely separable — an OK assumption if you ignore gravity and if your potential fields move slowly relative to the speed of light. Now read the section, follow the derivation, and go through the worked problems. Most useful applications of QM can be derived using this time-independent version of Schrödinger’s wave equation.

Musical Color and the Well Tempered Scale

5 Replies

by R. E. Buxbaum, (the author of all these posts)

I first heard J. S. Bach’s Well Tempered Clavier some 35 years ago and was struck by the different colors of the different scales. Some were dark and scary, others were light and enjoyable. All of them worked, but each was distinct, though I could not figure out why. That Bach was able to write in all the keys without retuning was a key innovation of his. In his day, people tuned in fifths, a process that created gaps (called wolf) that prevented useful composition in affected keys.

We don’t know exactly how Bach tuned his instruments as he had no scientific way to describe it; we can guess that it was more uniform than the temper produced by tuning in fifths, but it probably was not quite equally spaced. Nowadays electronic keyboards are tuned to 12 equally spaced frequencies per octave through the use of frequency counters.  Starting with the A below “middle C”, A4, tuned at 440 cycles/second (the note symphonies tune to), each note is programmed to vibrate at a wavelength that is lower or higher than one next to it by a factor of the twelfth root of two, 12√2= 1.05946. After 12 multiples of this size, the wavelength has doubled or halved and there is an octave. This is called equal tempering.

Currently, many non-electric instruments are also tuned this way.  Equally tempering avoids all wolf, but makes each note equally ill-tempered. Any key can be transposed to another, but there are no pure harmonies because 12√2 is an irrational number (see joke). There is also no color or feel to any given key except that which has carried over historically in the listeners’ memory. It’s sad.

I’m going to speculate that J.S. Bach found/ favored a way to tune instruments where all of the keys were usable, and OK sounding, but where some harmonies are more perfect than others. Necessarily this means that some harmonies will be less-perfect. There should be no wolf gaps that would sound so bad that Bach could not compose and transpose in every key, but since there is a difference, each key will retain a distinct color that JS Bach explored in his work — or so I’ll assume.

Pythagoras found that notes sound best together when the vibrating lengths are kept in a ratio of small numbers. Consider the tuning note, A4, the A below middle C; this note vibrates a column of air .784 meters long, about 2.5 feet or half the length of an oboe. The octave notes for A4 are called A3 and A5. They vibrate columns of air 2x as long and 1/2 as long as the original. They’re called octaves because they’re eight white keys away from A4. Keyboards add 4 black notes per octave so octaves are always 12 notes away. Keyboards are generally tuned so octaves are always 12 keys away. Based on Pythagoras, a reasonable presumption is that J.S Bach tuned every non-octave note so that it vibrates an air column similar to the equal tuning ratio, 12√2 = 1.05946, but whose wavelength was adjusted, in some cases to make ratios of small, whole numbers with the wavelength for A4.

Aside from octaves, the most pleasant harmonies are with notes whose wavelength is 3/2 as long as the original, or 2/3 as long. The best harmonies with A4 (0.784 m) will be with notes with wavelengths (3/2)*0.784 m long, or (2/3)*0.784m long. The first of these is called D3 and the other is E4. A4 combines with D3 to make a chord called D-major, the so-called “the key of glory.” The Hallelujah chorus, Beethoven’s 9th (Ode to Joy), and Mahler’s Titan are in this key. Scriabin believed that D-major had a unique color, gold, suggesting that the pure ratios were retained.

A combines with E (plus a black note C#) to make a chord called A major. Songs in this key sound (to my ear) robust, cheerful and somewhat pompous; Here, in A-major is: Dancing Queen by ABBA, Lady Madonna by the Beatles; Prelude and Fugue in A major by JS Bach. Scriabin believed that A-major was green.

A4 also combines with E and a new white note, C3, to make a chord called A minor. Since E4 and E3 vibrate at 2/3 and 4/3 the wavelength of A4 respectively, I’ll speculate that Bach tuned C3 to 5/3 the length of A4; 5/3*.0784m =1.307m long. Tuned his way, the ratio of wavelengths in the A minor chord are 3:4:5. Songs in A minor tend to be edgy and sort-of sad: Stairway to heaven, Für Elise, “Songs in A Minor sung by Alicia Keys, and PDQ Bach’s Fugue in A minor. I’m going to speculate the Bach tuned this to 1.312 m (or thereabouts), roughly half-way between the wavelength for a pure ratio and that of equal temper.

The notes D3 and E3 will not sound particularly good together. In both pure ratios and equal tempers their wavelengths are in a ratio of 3/2 to 4/3, that is a ratio of 9 to 8. This can be a tensional transition, but it does not provide a satisfying resolution to my, western ears.

Now for the other white notes. The next white key over from A4 is G3, two half-tones longer that for A4. For equal tuning, we’d expect this note to vibrate a column of air 1.059462 = 1.1225 times longer than A4. The most similar ratio of small whole numbers is 9/8 = 1.1250, and we’d already generated one before between D and E. As a result, we may expect that Bach tuned G3 to a wavelength 9/8*0.784m = .88 meters.

For equal tuning, the next white note, F3, will vibrate an air column 1.059464 = 1.259 times as long as the A4 column. Tuned this way, the wavelength for F3 is 1.259*.784 = .988m. Alternately, since 1.259 is similar to 5/4 = 1.25, it is reasonable to tune F3 as (5/4)*.784 = .980m. I’ll speculate that he split the difference: .984m. F, A, and C combine to make a good harmony called the F major chord. The most popular pieces in F major sound woozy and not-quite settled in my opinion, perhaps because of the oddness of the F tuning. See, e.g. the Jeopardy theme song, “My Sweet Lord,” Come together (Beetles), Beethoven’s Pastoral symphony (Movement 1, “Awakening of cheerful feelings upon arrival in the country”). Scriabin saw F-major as bright blue.

We’ve only one more white note to go in this octave: B4, the other tension note to A4. Since the wavelengths for G3 was 9/8 as long as for A4, we can expect the wavelength for B4 will be 8/9 as long. This will be dissonant to A4, but it will go well with E3 and E4 as these were 2/3 and 4/3 of A4 respectively. Tuned this way, B4 vibrates a column 1.40 m. When B, in any octave, is combined with E it’s called an E chord (E major or E minor); it’s typically combined with a black key, G-sharp (G#). The notes B, E vibrate at a ratio of 4 to 3. J.S. Bach called the G#, “H” allowing him to spell out his name in his music. When he played the sequence BACH, he found B to A created tension; moving to C created harmony with A, but not B, while the final note, G# (H) provided harmony for C and the original B. Here’s how it works on cello; it’s not bad, but there is no grand resolution. The Promenade from “Pictures at an Exhibition” is in E.

The black notes go somewhere between the larger gaps of the white notes, and there is a traditional confusion in how to tune them. One can tune the black notes by equal temper  (multiples of 21/12), or set them exactly in the spaces between the white notes, or tune them to any alternate set of ratios. A popular set of ratios is found in “Just temper.” The black note 6 from A4 (D#) will have wavelength of 0.784*26/12= √2 *0.784 m =1.109m. Since √2 =1.414, and that this is about 1.4= 7/5, the “Just temper” method is to tune D# to 1.4*.784m =1.098m. If one takes this route, other black notes (F#3 and C#3) will be tuned to ratios of 6/5, and 8/5 times 0.784m respectively. It’s possible that J.S. Bach tuned his notes by Just temper, but I suspect not. I suspect that Bach tuned these notes to fall in-between Just Temper and Equal temper, as I’ve shown below. I suspect that his D#3 might vibrated at about 1.104 m, half way between Just and Equal temper. I would not be surprised if Jazz musicians tuned their black notes more closely to the fifths of Just temper: 5/5 6/5, 7/5, 8/5 (and 9/5?) because jazz uses the black notes more, and you generally want your main chords to sound in tune. Then again, maybe not. Jimmy Hendrix picked the harmony D#3 with A (“Diabolus”, the devil harmony) for his Purple Haze; it’s also used for European police sirens.

To my ear, the modified equal temper is more beautiful and interesting than the equal temperament of todays electronic keyboards. In either temper music plays in all keys, but with an un-equal temper each key is distinct and beautiful in its own way. Tuning is engineering, I think, rather than math or art. In math things have to be perfect; in art they have to be interesting, and in engineering they have to work. Engineering tends to be beautiful its way. Generally, though, engineering is not perfect.

Summary of air column wave-lengths, measured in meters, and as a ratio to that for A4. Just Tempering, Equal Tempering, and my best guess of J.S. Bach's Well Tempered scale.

Summary of air column wave-lengths, measured in meters, and as a ratio to that for A4. Just Tempering, Equal Tempering, and my best guess of J.S. Bach’s Well Tempered scale.

R.E. Buxbaum, May 20 2013 (edited Sept 23, 2013) — I’m not very musical, but my children are.

Chaos, Stocks, and Global Warming

14 Replies

Two weeks ago, I discussed black-body radiation and showed how you calculate the rate of radiative heat transfer from any object. Based on this, I claimed that basal metabolism (the rate of calorie burning for people at rest) was really proportional to surface area, not weight as in most charts. I also claimed that it should be near-impossible to lose weight through exercise, and went on to explain why we cover the hot parts of our hydrogen purifiers and hydrogen generators in aluminum foil.

I’d previously discussed chaos and posted a chart of the earth’s temperature over the last 600,000 years. I’d now like to combine these discussions to give some personal (R. E. Buxbaum) thoughts on global warming.

Black-body radiation differs from normal heat transfer in that the rate is proportional to emissivity and is very sensitive to temperature. We can expect the rate of heat transfer from the sun to earth will follow these rules, and that the rate from the earth will behave similarly.

That the earth is getting warmer is seen as proof that the carbon dioxide we produce is considered proof that we are changing the earth’s emissivity so that we absorb more of the sun’s radiation while emitting less (relatively), but things are not so simple. Carbon dioxide should, indeed promote terrestrial heating, but a hotter earth should have more clouds and these clouds should reflect solar radiation, while allowing the earth’s heat to radiate into space. Also, this model would suggest slow, gradual heating beginning, perhaps in 1850, but the earth’s climate is chaotic with a fractal temperature rise that has been going on for the last 15,000 years (see figure).

Recent temperature variation as measured from the Greenland Ice. A previous post had the temperature variation over the past 600,000 years.

Recent temperature variation as measured from the Greenland Ice. Like the stock market, it shows aspects of chaos.

Over a larger time scale, the earth’s temperature looks, chaotic and cyclical (see the graph of global temperature in this post) with ice ages every 120,000 years, and chaotic, fractal variation at times spans of 100 -1000 years. The earth’s temperature is self-similar too; that is, its variation looks the same if one scales time and temperature. This is something that is seen whenever a system possess feedback and complexity. It’s seen also in the economy (below), a system with complexity and feedback.

Manufacturing Profit is typically chaotic -- something that makes it exciting.

Manufacturing Profit is typically chaotic — and seems to have cold spells very similar to the ice ages seen above.

The economy of any city is complex, and the world economy even more so. No one part changes independent of the others, and as a result we can expect to see chaotic, self-similar stock and commodity prices for the foreseeable future. As with global temperature, the economic data over a 10 year scale looks like economic data over a 100 year scale. Surprisingly,  the economic data looks similar to the earth temperature data over a 100 year or 1000 year scale. It takes a strange person to guess either consistently as both are chaotic and fractal.

gomez3

It takes a rather chaotic person to really enjoy stock trading (Seen here, Gomez Addams of the Addams Family TV show).

Clouds and ice play roles in the earth’s feedback mechanisms. Clouds tend to increase when more of the sun’s light heats the oceans, but the more clouds, the less heat gets through to the oceans. Thus clouds tend to stabilize our temperature. The effect of ice is to destabilize: the more heat that gets to the ice, the more melts and the less of the suns heat is reflected to space. There is time-delay too, caused by the melting flow of ice and ocean currents as driven by temperature differences among the ocean layers, and (it seems) by salinity. The net result, instability and chaos.

The sun has chaotic weather too. The rate of the solar reactions that heat the earth increases with temperature and density in the sun’s interior: when a volume of the sun gets hotter, the reaction rates pick up making the volume yet-hotter. The temperature keeps rising, and the heat radiated to the earth keeps increasing, until a density current develops in the sun. The hot area is then cooled by moving to the surface and the rate of solar output decreases. It is quite likely that some part of our global temperature rise derives from this chaotic variation in solar output. The ice caps of Mars are receding.

The change in martian ice could be from the sun, or it might be from Martian dust in the air. If so, it suggests yet another feedback system for the earth. When economic times age good we have more money to spend on agriculture and air pollution control. For all we know, the main feedback loops involve dust and smog in the air. Perhaps, the earth is getting warmer because we’ve got no reflective cloud of dust as in the dust-bowl days, and our cities are no longer covered by a layer of thick, black (reflective) smog. If so, we should be happy to have the extra warmth.

The Gift of Chaos

7 Replies

Many, if not most important engineering systems are chaotic to some extent, but as most college programs don’t deal with this behavior, or with this type of math, I thought I might write something on it. It was a big deal among my PhD colleagues some 30 years back as it revolutionized the way we looked at classic problems; it’s fundamental, but it’s now hardly mentioned.

Two of the first freshman engineering homework problems I had turn out to have been chaotic, though I didn’t know it at the time. One of these concerned the cooling of a cup of coffee. As presented, the coffee was in a cup at a uniform temperature of 70°C; the room was at 20°C, and some fanciful data was presented to suggest that the coffee cooled at a rate that was proportional the difference between the (changing) coffee temperature and the fixed room temperature. Based on these assumptions, we predicted exponential cooling with time, something that was (more or less) observed, but not quite in real life. The chaotic part in a real cup of coffee, is that the cup develops currents that move faster and slower. These currents accelerate heat loss, but since they are driven by the temperature differences within the cup they tend to speed up and slow down erratically. They accelerate when the cup is not well stirred, causing new stir, and slow down when it is stirred, and the temperature at any point is seen to rise and fall in an almost rhythmic fashion; that is, chaotically.

While it is impossible to predict what will happen over a short time scale, there are some general patterns. Perhaps the most remarkable of these is self-similarity: if observed over a short time scale (10 seconds or less), the behavior over 10 seconds will look like the behavior over 1 second, and this will look like the behavior over 0.1 second. The only difference being that, the smaller the time-scale, the smaller the up-down variation. You can see the same thing with stock movements, wind speed, cell-phone noise, etc. and the same self-similarity can occur in space so that the shape of clouds tends to be similar at all reasonably small length scales. The maximum average deviation is smaller over smaller time scales, of course, and larger over large time-scales, but not in any obvious way. There is no simple proportionality, but rather a fractional power dependence that results in these chaotic phenomena having fractal dependence on measure scale. Some of this is seen in the global temperature graph below.

Global temperatures measured from the antarctic ice showing stable, cyclic chaos and self-similarity.

Global temperatures measured from the antarctic ice showing stable, cyclic chaos and self-similarity.

Chaos can be stable or unstable, by the way; the cooling of a cup of coffee was stable because the temperature could not exceed 70°C or go below 20°C. Stable chaotic phenomena tend to have fixed period cycles in space or time. The world temperature seems to follow this pattern though there is no obvious reason it should. That is, there is no obvious maximum and minimum temperature for the earth, nor any obvious reason there should be cycles or that they should be 120,000 years long. I’ll probably write more about chaos in later posts, but I should mention that unstable chaos can be quite destructive, and quite hard to prevent. Some form of chaotic local heating seems to have caused battery fires aboard the Dreamliner; similarly, most riots, famines, and financial panics seem to be chaotic. Generally speaking, tight control does not prevent this sort of chaos, by the way; it just changes the period and makes the eruptions that much more violent. As two examples, consider what would happen if we tried to cap a volcano, or provided  clamp-downs on riots in Syria, Egypt or Ancient Rome.

From math, we know some alternate ways to prevent unstable chaos from getting out of hand; one is to lay off, another is to control chaotically (hard to believe, but true).

 

Statistics Joke

A classic statistics joke concerns a person who’s afraid to fly; he goes to a statistician who explains that planes are very, very safe, especially if you fly a respectable airline in good weather. In that case, virtually the only problem you’ll have is the possibility of a bomb on board. The fellow thinks it over and decides that flying is still too risky, so the statistician suggests he plant a bomb on the airplane, but rig it to not go off. The statistician explains: while it’s very rare to have a bomb onboard an airplane, it’s really unheard of to have two bombs on the same plane.

It’s funny because …. the statistician left out the fact that an independent variable (number of bombs) has to be truly independent. If it is independent, the likelihood is found using a poisson distribution, a non-normal distribution where the greatest likelihood is zero bombs, and there are no possibilities for a negative bomb. Poisson distributions are rarely taught in schools for some reason.

By Dr. Robert E. Buxbaum, Mar 25, 2013. If you’ve got a problem like this (particularly involving chemical engineering) you could come to my company, REB Research.

Heat conduction in insulating blankets, aerogels, space shuttle tiles, etc.

4 Replies

A lot about heat conduction in insulating blankets can be explained by the ordinary motion of gas molecules. That’s because the thermal conductivity of air (or any likely gas) is much lower than that of glass, alumina, or any likely solid material used for the structure of the blanket. At any temperature, the average kinetic energy of an air molecule is 1/2kT in any direction, or 3/2kT altogether; where k is Boltzman’s constant, and T is absolute temperature, °K. Since kinetic energy equals 1/2 mv2, you find that the average velocity in the x direction must be v = √kT/m = √RT/M. Here m is the mass of the gas molecule in kg, M is the molecular weight also in kg (0.029 kg/mol for air), R is the gas constant 8.29J/mol°C, and v is the molecular velocity in the x direction, in meters/sec. From this equation, you will find that v is quite large under normal circumstances, about 290 m/s (650 mph) for air molecules at ordinary temperatures of 22°C or 295 K. That is, air molecules travel in any fixed direction at roughly the speed of sound, Mach 1 (the average speed including all directions is about √3 as fast, or about 1130 mph).

The distance a molecule will go before hitting another one is a function of the cross-sectional areas of the molecules and their densities in space. Dividing the volume of a mol of gas, 0.0224 m3/mol at “normal conditions” by the number of molecules in the mol (6.02 x10^23) gives an effective volume per molecule at this normal condition: .0224 m3/6.0210^23 = 3.72 x10^-26 m3/molecule at normal temperatures and pressures. Dividing this volume by the molecular cross-section area for collisions (about 1.6 x 10^-19 m2 for air based on an effective diameter of 4.5 Angstroms) gives a free-motion distance of about 0.23×10^-6 m or 0.23µ for air molecules at standard conditions. This distance is small, to be sure, but it is 1000 times the molecular diameter, more or less, and as a result air behaves nearly as an “ideal gas”, one composed of point masses under normal conditions (and most conditions you run into). The distance the molecule travels to or from a given surface will be smaller, 1/√3 of this on average, or about 1.35×10^-7m. This distance will be important when we come to estimate heat transfer rates at the end of this post.

 

Molecular motion of an air molecule (oxygen or nitrogen) as part of heat transfer process; this shows how some of the dimensions work.

Molecular motion of an air molecule (oxygen or nitrogen) as part of heat transfer process; this shows how some of the dimensions work.

The number of molecules hitting per square meter per second is most easily calculated from the transfer of momentum. The pressure at the surface equals the rate of change of momentum of the molecules bouncing off. At atmospheric pressure 103,000 Pa = 103,000 Newtons/m2, the number of molecules bouncing off per second is half this pressure divided by the mass of each molecule times the velocity in the surface direction. The contact rate is thus found to be (1/2) x 103,000 Pa x 6.02^23 molecule/mol /(290 m/s. x .029 kg/mol) = 36,900 x 10^23 molecules/m2sec.

The thermal conductivity is merely this number times the heat capacity transfer per molecule times the distance of the transfer. I will now calculate the heat capacity per molecule from statistical mechanics because I’m used to doing things this way; other people might look up the heat capacity per mol and divide by 6.02 x10^23: For any gas, the heat capacity that derives from kinetic energy is k/2 per molecule in each direction, as mentioned above. Combining the three directions, that’s 3k/2. Air molecules look like dumbbells, though, so they have two rotations that contribute another k/2 of heat capacity each, and they have a vibration that contributes k. We begin with an approximate value for k = 2 cal/mol of molecules per °C; it’s actually 1.987 but I round up to include some electronic effects. Based on this, we calculate the heat capacity of air to be 7 cal/mol°C at constant volume or 1.16 x10^-23 cal/molecule°C. The amount of energy that can transfer to the hot (or cold) wall is this heat capacity times the temperature difference that molecules carry between the wall and their first collision with other gases. The temperature difference carried by air molecules at standard conditions is only 1.35 x10-7 times the temperature difference per meter because the molecules only go that far before colliding with another molecule (remember, I said this number would be important). The thermal conductivity for stagnant air per meter is thus calculated by multiplying the number of molecules times that hit per m2 per second, the distance the molecule travels in meters, and the effective heat capacity per molecule. This would be 36,900 x 10^23  molecules/m2sec x 1.35 x10-7m x 1.16 x10^-23 cal/molecule°C = 0.00578 cal/ms°C or .0241 W/m°C. This value is (pretty exactly) the thermal conductivity of dry air that you find by experiment.

I did all that math, though I already knew the thermal conductivity of air from experiment for a few reasons: to show off the sort of stuff you can do with simple statistical mechanics; to build up skills in case I ever need to know the thermal conductivity of deuterium or iodine gas, or mixtures; and finally, to be able to understand the effects of pressure, temperature and (mainly insulator) geometry — something I might need to design a piece of equipment with, for example, lower thermal heat losses. I find, from my calculation that we should not expect much change in thermal conductivity with gas pressure at near normal conditions; to first order, changes in pressure will change the distance the molecule travels to exactly the same extent that it changes the number of molecules that hit the surface per second. At very low pressures or very small distances, lower pressures will translate to lower conductivity, but for normal-ish pressures and geometries, changes in gas pressure should not affect thermal conductivity — and does not.

I’d predict that temperature would have a larger effect on thermal conductivity, but still not an order-of magnitude large effect. Increasing the temperature increases the distance between collisions in proportion to the absolute temperature, but decreases the number of collisions by the square-root of T since the molecules move faster at high temperature. As a result, increasing T has a √T positive effect on thermal conductivity.

Because neither temperature nor pressure has much effect, you might expect that the thermal conductivity of all air-filed insulating blankets at all normal-ish conditions is more-or-less that of standing air (air without circulation). That is what you find, for the most part; the same 0.024 W/m°C thermal conductivity with standing air, with high-tech, NASA fiber blankets on the space shuttle and with the cheapest styrofoam cups. Wool felt has a thermal conductivity of 0.042 W/m°C, about twice that of air, a not-surprising result given that wool felt is about 1/2 wool and 1/2 air.

Now we can start to understand the most recent class of insulating blankets, those with very fine fibers, or thin layers of fiber (or aluminum or gold). When these are separated by less than 0.2µ you finally decrease the thermal conductivity at room temperature below that for air. These layers decrease the distance traveled between gas collisions, but still leave the same number of collisions with the hot or cold wall; as a result, the smaller the gap below .2µ the lower the thermal conductivity. This happens in aerogels and some space blankets that have very small silica fibers, less than .1µ apart (<100 nm). Aerogels can have much lower thermal conductivities than 0.024 W/m°C, even when filled with air at standard conditions.

In outer space you get lower thermal conductivity without high-tech aerogels because the free path is very long. At these pressures virtually every molecule hits a fiber before it hits another molecule; for even a rough blanket with distant fibers, the fibers bleak up the path of the molecules significantly. Thus, the fibers of the space shuttle (about 10 µ apart) provide far lower thermal conductivity in outer space than on earth. You can get the same benefit in the lab if you put a high vacuum of say 10^-7 atm between glass walls that are 9 mm apart. Without the walls, the air molecules could travel 1.3 µ/10^-7 = 13m before colliding with each other. Since the walls of a typical Dewar are about 0.009 m apart (9 mm) the heat conduction of the Dewar is thus 1/150 (0.7%) as high as for a normal air layer 9mm thick; there is no thermal conductivity of Dewar flasks and vacuum bottles as such, since the amount of heat conducted is independent of gap-distance. Pretty spiffy. I use this knowledge to help with the thermal insulation of some of our hydrogen generators and hydrogen purifiers.

There is another effect that I should mention: black body heat transfer. In many cases black body radiation dominates: it is the reason the tiles are white (or black) and not clear; it is the reason Dewar flasks are mirrored (a mirrored surface provides less black body heat transfer). This post is already too long to do black body radiation justice here, but treat it in more detail in another post.

RE. Buxbaum