Category Archives: Science: Physics, Astronomy, etc.

Why isn’t the sky green?

14 Replies

Yesterday I blogged with a simple version of why the sky was blue and not green. Now I’d like to add mathematics to the treatment. The simple version said that the sky was blue because the sun color was a spectrum centered on yellow. I said that molecules of air scattered mostly the short wavelength, high frequency light colors, indigo and blue. This made the sky blue. I said that, the rest of the sunlight was not scattered, so that the sun looked yellow. I then said that the only way for the sky to be green would be if the sun were cooler, orange say, then the sky would be green. The answer is sort-of true, but only in a hand-waving way; so here’s the better treatment.

Light scatters off of dispersed small particles in proportion to wavelength to the inverse 4th power of the wavelength. That is to say, we expect air molecules will scatter more short wavelength, cool colors (purple and indigo) than warm colors (red and orange) but a real analysis must use the actual spectrum of sunlight, the light power (mW/m2.nm) at each wavelength.

intensity of sunlight as a function of wavelength (frequency)

intensity of sunlight as a function of wavelength

The first thing you’ll notice is that the light from our sun isn’t quite yellow, but is mostly green. Clearly plants understand this, otherwise chlorophyl would be yellow. There are fairly large components of blue and red too, but my first correction to the previous treatment is that the yellow color we see as the sun is a trick of the eye called additive color. Our eyes combine the green and red of the sun’s light, and sees it as yellow. There are some nice classroom experiment you can do to show this, the simplest being to make a Maxwell top with green and red sections, spin the top, and notice that you see the color as yellow.

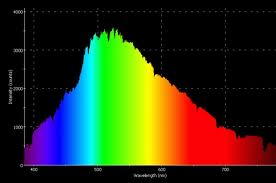
In order to add some math to the analysis of sky color, I show a table below where I divided the solar spectrum into the 7 representative colors with their effective power. There is some subjectivity to this, but I took red as the wavelengths from 620 to 750nm so I claim on the table was 680 nm. The average power of the red was 500 mW/m2nm, so I calculate the power as .5 W/m2nm x 130 nm = 65W/m2. Similarly, I took orange to be the 30W/m2 centered on 640nm, etc. This division is presented in the first 3 columns of the following table. The first line of the table is an approximate of the Rayleigh-scatter factor for our atmosphere, with scatter presented as the percent of the incident light. That is % scattered = 9E11/wavelength^4.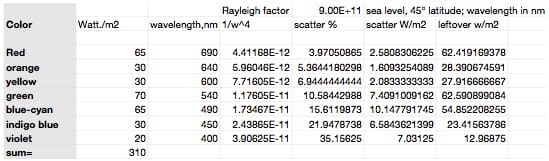skyblue scatter

To use the Rayleigh factor, I calculate the 1/wavelength of each color to the 4th power; this is shown in the 4th column. The scatter % is now calculated and I apply this percent to the light intensities to calculate the amount of each color that I’d expect in the scattered and un-scattered light (the last two columns). Based on this, I find that the predominant wavelength in the color of the sky should be blue-cyan with significant components of green, indigo, and violet. When viewed through a spectroscope, I find that these are the colors I see (I have a pocket spectroscope and used it an hour ago to check). Viewed through the same spectroscope (with eye protection), I expect the sun should look like a combination of green and red, something our eyes see as yellow (I have not done this personally). At any rate, it appears that the sky looks blue because our eyes see the green+ cyan+ indigo + purple in the scattered light as sky blue.220px-RGB_illumination

At sunrise and sunset when the sun is on the horizon the scatter percents will be higher, so that all of the sun’s colors will be scattered except red and orange. The sun looks orange then, as expected, but the sky should look blue-green, as that’s the combination of all the other colors of sunlight when orange and red are removed. I’ve not checked this last yet. I’ll have to take my spectroscope to a fine sunset and see what I see when I look at the sky.

Why isn’t the sky green and the sun orange?

5 Replies

Part of the reason the sky isn’t green has to do with the color of the sun. The sun’s color, and to a lesser extent, the sky color both are determined by the sun’s surface color, yellow. This surface color results from black body radiation: if you heat up a black object it will first glow red, then orange, yellow, green etc. Red is a relatively cool color because it’s a low frequency (long wavelength) and low frequencies are the lowest energy photons, and thus are the easiest for a black body to produce. As one increases the temperature of a black object, the total number of photons increases for all wavelengths, but the short wavelength (high frequency) colors increase faster than the of long wavelength colors. As a result, the object is seen to change color to orange, then yellow, or to any other color representative of objects at that particular temperature.

Our star is called a yellow sun because the center color of its radiation is yellow. The sun provides radiation in all colors and wavelengths, even colors invisible to the eye, infra red and ultra violet, but because of its temperature, most of the radiated energy appears as yellow. This being said, you may wonder why the sky isn’t yellow (the sky of Mars mostly is).

The reason the sky is blue, is that some small fraction of the light of the sun (about 10%) scatters off of the molecules of the air. This is called Rayleigh scatter — the scatter of large wavelegth waves off of small objects.  The math for this will be discussed in another post, but the most relevant aspect here is that the fraction that is scattered is proportional to the 4th power of the frequency. This is to say, that the high frequencies (blue, indigo, and violet) scatter a lot, about 20%, while the red hardly scatters at all. As a result the sky has a higher frequency color than the sun does. In our case, the sky looks blue, while the sun looks slightly redder from earth than it does from space — at least that’s the case for most of the day.

The sun looks orange-red at sundown because the sunlight has to go through more air. Because of this, a lot more of the yellow, green, and blue scatter away before we see it. Much more of the scatter goes off into space, with the result that the sky to looks dark, and somewhat more greenish at sundown. If the molecules were somewhat bigger, we’d still see a blue sky, maybe somewhat greener, with a lot more intensity. That’s the effect that carbon dioxide has — it causes more sunlight to scatter, making the sky brighter. If the sun were cooler (orange say), the sky would appear green. That’s because there would be less violet and blue in the sunlight, and the sky color would be shifted to the longer wavelengths. On planets where the sun is cooler than ours, the sky is likely green, but could be yellow or red.

Rayleigh scatter requires objects that are much smaller than the light wavelength. A typical molecule of air is about 1 nm in size (1E-9 of a meter), while the wavelength of yellow light is 580 nm. That’s much larger than the size of air molecules. Snow appears white because the size of the crystals are the size of the sun wavelengths, tor bigger, 500-2000 nm. Thus, the snow looks like all the colors of the sun together, and that’s white. White = the sum of all the colors: red + orange + blue + green + yellow + violet + indigo.

Robert Buxbaum  Jan. 27, 2013 (revised)

What causes the swirl of tornadoes and hurricanes

10 Replies

Some weeks ago, I presented an explanation of why tornadoes and hurricanes pick up stuff based on an essay by A. Einstein that explained the phenomenon in terms of swirling fluids and Coriolis flows. I put in my own description that I thought was clearer since it avoided the word “Coriolis”, and attached a video so you could see how it all worked — or rather that is was as simple as all that. (Science teachers: I’ve found kids love it when I do this, and similar experiments with centrifugal force in the class-room as part of a weather demonstration).

I’d like to now answer a related question that I sometimes get: where does the swirl come from? hurricanes that answer follows, though I think you’ll find my it is worded differently from that in Wikipedia and kids’ science books since (as before) I don’t use the word Coriolis, nor any other concept beyond conservation of angular momentum plus that air flows from high pressure to low.

In Wikipedia and all the other web-sits I visited, it was claimed that the swirl came from “Coriolis force.” While this isn’t quite wrong, I find this explanation incomprehensible and useless. Virtually no-one has a good feel for Coriolis force as such, and those who do recognize that it doesn’t exist independently like gravity. So here is my explanation based on low and high pressure and on conservation of angular momentum.  I hope it will be clearer.

All hurricanes are associated with low pressure zones. This is not a coincidence as I understand it, but a cause-and-effect relationship. The low pressure center is what causes the hurricane to form and grow. It may also cause tornadoes but the relationship seems less clear. In the northern hemisphere, the lowest low pressure zones are found to form over the mid Atlantic or Pacific in the fall because the water there is warm and that makes the air wet and hot. Static air pressure is merely the weight of the air over a certain space, and as hot air has more volume and less density, it weighs less. Less weight = less pressure, all else being equal. Adding water (humidity) to air also reduces the air pressure as the density of water vapor is less than that of dry air in proportion to their molecular weights. The average molecular weight of dry air is 29 and the molecular weight of water is 18. As a result, every 9% increase in water content decreases the air pressure by 1% (7.6 mm or 0.3″ of mercury).

Air tends to flow from high pressure zones to low pressure zones. In the northern hemisphere, some of the highest high pressure zones form over northern Canada and Russia in the winter. High pressure zones form there by the late fall because these regions are cold and dry. Cold air is less voluminous than hot, and as a result additional hot air flows into these zones at high altitude. At sea level the air flows out from the high pressure zones to the low pressure zones and begins to swirl because of conservation of angular momentum.

All the air in the world is spinning with the earth. At the north pole the spin rate is 360 degrees every 24 hours, or 15 degrees per hour. The spin rate is slower further south, proportionally to the sine of the latitude, and it is zero at the equator. The spin of the earth at your location is observable with a Foucault pendulum (there is likely to be one found in your science museum). We normally don’t notice the spin of the air around us because the earth is spinning at the same rate, normally. However the air has angular momentum, and when air moves into into a central location the angular speed increases because the angular momentum must be conserved. As the gas moves in, the spin rate must increase in proportion; it eventually becomes noticeable relative to the earth’s spin. Thus, if the air starts out moving at 10 degrees per hour (that’s the spin rate in Detroit, MI 41.8° N), and moves from 800 miles away from a low pressure center to only 200 miles from the center, the angular momentum must increase four times, or to 40 degrees per hour. We would only see 30 degrees/hr of this because the earth is spinning, but the velocity this involves is significant: V= 200 miles * 2* pi *30/360 = 104 mph.

To give students a sense of angular momentum conservation, most science centers (and colleges) use an experiment involving bicycle wheels and a swivel chair. In the science centers there is usually no explanation of why, but in college they tend to explain it in terms of vectors and (perhaps) gauge theories of space-time (a gauge is basically a symmetry; angular momentum is conserved because space is symmetric in rotation). In a hurricane, the air at sea level always spins in the same direction of the earth: counter clockwise in the northern hemisphere, clockwise in the southern, but it does not spin this way forever.

The air that’s sucked into the hurricane become heated and saturated with water. As a result, it becomes less dense, expands, and rises, sucking fresh air in behind it. As the hot wet air rises it cools and much of the water rains down as rain. When the, now dry air reaches a high enough altitude its air pressure is higher than that above the cold regions of the north; the air now flows away north. Because this hot wet air travels north we typically get rain in Michigan when the Carolinas are just being hit by hurricanes. As the air flows away from the centers at high altitudes it begins to spin the opposite direction, by the way, so called counter-cyclonally because angular momentum has to be consevered. At high altitudes over high pressure centers I would expect to find cyclones too (spinning cyclonally) I have not found a reference for them, but suspect that airline pilots are aware of the effect. There is some of this spin at low altitudes, but less so most of the time.

Hurricanes tend to move to the US and north through the hurricane season because, as I understand it, the cold air that keeps coming to feed the hurricane comes mostly from the coastal US. As I understand it the hurricane is not moving as such, the air stays relatively stationary and the swirl that we call a hurricane moves to the US in the effective direction of the sea-level air flow.

For tornadoes, I’m sorry to say, this explanation does not work quite as well, and Wikipedia didn’t help clear things up for me either. The force of tornadoes is much stronger than of hurricanes (the swirl is more concentrated) and the spin direction is not always cyclonic. Also tornadoes form in some surprising areas like Kansas and Michigan where hurricanes never form. My suspicion is that most, but not all tornadoes form from the same low pressure as hurricanes, but by dry heat, not wet. Tornadoes form in Michigan, Texas, and Alabama in the early summer when the ground is dry and warmer than the surrounding lakes and seas. It is not difficult to imagine the air rising from the hot ground and that a cool wind would come in from the water and beginning to swirl. The cold, damp sea air would be more dense than the hot, dry land air, and the dry air would rise. I can imagine that some of these tornadoes would occur with rain, but that many the more intense?) would have little or none; perhaps rain-fall tends to dampen the intensity of the swirl (?)

Now we get to things that I don’t have good explanation for at all: why Kansas? Kansas isn’t particularly hot or cold; it isn’t located near lakes or seas, so why do they have so many tornadoes? I don’t know. Another issue that I don’t understand: why is it that some tornadoes rotate counter cyclonicly? Wikipedia says these tornadoes shed from other tornadoes, but this doesn’t quite seem like an explanation. My guess is that these tornadoes are caused by a relative high pressure source at ground level (a region of cold ground for example) coupled with a nearby low pressure zone (a warm lake?). My guess is that this produces an intense counter-cyclonic flow to the low pressure zone. As for why the pressure is very low in tornadoes, even these that I think are caused by high pressure, I suspect the intense low pressure is an epee-phenomenon caused by the concentration of spin — one I show in my video. That is, I suspect that the low pressure in the center of counter-cyclonic tornadoes is not the cause of the tornado but an artifact of the concentrated spin. Perhaps I’m wrong here, but that’s the explanation that seems to fit best with the info I’ve got. If you’ve got better explanations for these two issues, I’d love to hear them.

The joy of curtains

8 Replies

By Dr. Robert E. Buxbaum January 18, 2013

In our northern climates most homes have double-paned windows; they cost a fortune, and are a lot better than plain glass, but they still lose a lot of heat: far more than the equivalent area of wall. The insulation value is poor mostly because the thickness is low: a typical double pane window is only ½” thick. The glass panes have hardly any insulation value, so the majority of the insulation is the 0.3″ air space between them. Our outer walls, by contrast, are typically 6” thick filled with glass –wool. The wall is 12 times as thick as the window, and it turns out that the R value is about 12 times as great. Since window area is about 1/10 the wall area, we can expect that about half your homes heat goes out through the windows (about half the air-conditioner cooling in the summer too). A good trick to improve your home’s insulation, then, is to add curtains as this provides a fairly thick layer of stagnant air inside the room, right next to your windows.

To see how much you can save by adding curtains, it’s nice (for me, and my mind-set mostly) to talk in terms of R values. In the northern USA, the “R” value of a typical, well-insulated outer wall is about 24. What that means is that it takes 24°F and one square foot of wall to remove 1 BTU per hour. That is, the resistance to heat loss is 24 °F.hr.ft2/BTU. The R value for a typical double pane window is about 2 in the same units, and is only 1 if you have single panes. The insulating quality of our windows is so poor that, for many homes, more heat is lost through the windows than through the rest of the wall space.

To figure out how much heat is lost through your windows take the area in square feet multiply by a typical temperature differential (50°F might be typical in Michigan), and divide by the R value of your paned windows (1 or 2) depending on whether it’s single or double paned. Since heat costs about $10/MMBTU ($10 per million BTU) for a gas heated house, you can figure out what a small, 10 ft2 window costs a typical Michigan householder as follows, assuming a single pane (R=1):

Q = Area* ∆T/R = 10 ft2 * 50°F/1 = 500 BTU/hr. Here Q is the heat lost per unit time, ∆T is the temperature difference between the window surface and the room, and A is the ara of the window surface.

Since there are 24 hours in a day, and 30.5 days in a month the dollar cost of that window is 500*24*31.5*10/1,000,000 = $3.78/month. After a few years, you’ll have paid $200 for that small window in lost heat and another $200 in air conditioning.

A cheap solution is to add curtains, shades, or plastic of some sort. These should not be placed too close to the window, or you won’t have a decent air gap, nor so far that the air will not be static in the gap. For small gaps between the window glass and your plastic or curtain, the heat transfer rate is proportional to the thermal conductivity of air, k, and inversely proportional to the air gap distance, ∂.

Q = ∆T A k /∂.

R  = ∂/k.

The thermal conductivity of air, k, is about .024 BTU/ft. hr°F. We thus confirm that the the R-value for an air gap of 9/16” or 1/20 foot is about 2 in these units. Though the typical air gap between the glass is less, about .3″ there is some more stagnant air outside the glass an that counts towards the 9/16″ of stagnant air. The k value of glass or plastic is much higher than of air, so the layers of glass or plastic add almost nothing to the total heat transfer resistance.

Because the R value of glass and plastic is so low, if you cover your window with a layer of plastic sheet that touches the window, the insulation effect is basically zero. To get insulation value you want to use a gap between about ½” and 1” in thickness. If you already have a 2 paned window of R value 2, you can expect to be able to raise your insulation value to 4 by adding a plastic sheet or single curtain at 9/16” from the glass.

Sorry to say, you can’t raise this insulation value much higher than 4 by use of a single air gap that’s more than 1″ thick. When a single gap exceeds this size, the insulating value drops dramatically as gas circulation in the gap (free convection) drives heat transfer. That’s why wall insulation has fiber-glass fill. For your home, you will want something more attractive than fiberglass between you and the window pane, and typical approaches  include cellular blinds or double layer drapes. These work on the same principle as the single sheet, but have extra layers that stop convection.

My favorite version of the double drapes is the federalist version, where the inner drape is near transparent, shim cloth hangs close to the window, with a heavier drape beyond that. The heavier curtain is closed at night and opened in daytime; where insulation is needed, the lighter cloth hangs day and night. This looks a lot better than a roll-type window shade, or bamboo screen. Besides, with a roll-shade or bamboo, you must put it close to the window where it will interfere with the convection flow, that is cold shedding from the shut window.

Another nice alternative is a “cell shade” These are folded lengths of two or more stiff cloths that are formed into honeycombs ½” to 2” apart. This empty thickness provides the insulating power of the shade. Placed at the right distance from the window, the cell shade will add 3 or more to the overall R value of the window (1/12 ft / .024 BTU/ft. hr°F = 3.5 ft2hr°F/BTU). As with a bamboo screen, all this R value goes away if the shade is set at more than about 1” from the window or an interior shade. At a greater thickness that this, the free convection flow of cold air between the window and the shade dominates, and you get a puddle of cold air on the floor. 

I would suggest a cellular shade that opens from the bottom only and is translucent. This provides light and privacy; a shade that is too dark will be left open. Behind this, my home has double-pane windows (when I was single the window was covered by a layer of plastic too). The see-through shade provides insulation while allowing one to see out the window (or let light in) when the shade is drawn. You want to be able to see out; that’s the reason you had a window in the first place. Very thick, insulating curtains and blinds seem like a waste to me – they are enough thicker to add any significant R-value, they block the light, and if they end up far from the window, the shedding heat loss will more than offset any small advantage from the thick cloth.

One last window insulation option that’s worth mentioning is a reflective coating on the glass (an e-coating). This is not as bad an idea as you might think, even in a cold climate as in Detroit. A surprising amount of heat tends to escape your windows in the form of radiation. That is, the heat leaves by way of invisible (infra –red) light that passes unimpeded through the double pane glass. In hot climates even more heat comes in this way, and a coating is even more useful to preserve air conditioning power. Reflective plastic coats are cheap enough and readily available, though they can be hard to apply, and are not always attractive.

You can expect to reduce the window heat loss by a factor of 3 or more using these treatments, reducing the heat loss through the small window to $1.00 or so per month, far enough that the main heat loss is through the walls. At that point, it may be worth putting your efforts elsewhere. Window treatments can save you money, make a previously uninhabitable room pleasant, and can help preserve this fair planet of ours. Enjoy.

Updated, Feb 9, 2022, REB.

Engineering joke

An optimist says the cup is half full.

A pessimist says the cup is half empty.

An engineer says the cup is twice as big as it has to be.

(A quantum physicist might say that the water isn’t in the cup till he looks at it; then again, the quantum physicist isn’t there until someone looks at him. And that’s why I’m an engineer).

How much wood could a woodchuck chuck?

“How much wood could a woodchuck chuck, if a woodchuck could chuck wood?” It’s a classic question with a simple answer: The woodchuck, also known as a groundhog or marmot, is a close relative to the beaver: it looks roughly the same, but is about 1/5 the weight  (10 pounds versus 50 pounds), and beavers do chuck wood, using their teeth to pull the logs and throw-pile it onto dams. I’ll call the tooth piling process chucking, since that’s what we would call it if a person did it by hand.

Beaver Dam

A beaver dam. From the size of this dam, and the rate of construction (one night) you can figure out how much wood a beaver could chuck, and from that how much a woodchuck could.

Based on the weight difference, my estimate is that a woodchuck would chuck about 1/5 as much wood as a beaver does. You might think this isn’t very much wood — and one “scientific” blogger claimed it would be less than 1/2 lb., but I’m certain he’s wrong. A beaver is able to build a dam like the one shown in a single night. Based on the size of the dam and the speed of building, we find that the beaver chucked about 1000 lbs of wood in a single night (beavers work at night). To figure out how much wood a woodchuck would chuck, divide this 5. I estimate that a woodchuck would chuck some 200 lbs per day, if it could and chose to.

Woodchucks don’t chuck wood, nor do they build dams or lodges. Instead they live in burrows in the ground. We have one living near my house. Woodchucks do kick up a lot of dirt digging a burrow, as much as 700 lb/day of dirt, but the question-language implies that this kicking activity should not be considered “chucking”. Well, now you know: it’s 200 lbs/night.

Robert Buxbaum. This post is revised January 30, 2020. My original estimate, from  January 2013 was half the value here. I’d come to believe that wood-chucks/ groundhogs are 1/10 the size of a beaver, so I’d estimated 100 lb/night. I now know they are heavier.

REB Research periodic table cup

2 Replies

Some 20 years ago I designed this periodic table cup, but with only the 103 named elements that existed then. In part this was done because I wanted a good, large, white coffee cup, in part because I often found I needed a periodic table, and didn’t like to have to look one up, and in part to people how much more area you get on a cylinder than on a flat sheet (roughly 3.14 times more area). To show that, I put all the side elements (rare earth lanthanides, and actinides) where they belonged, and not off on the side. I also put hydrogen in twice, once as a metal (HCl) and once as a non metal (NaH). The color I chose was Tryian Blue, a key color of Biblical Tyre, what you get from male purpura mollusks (the females give a shade of red that I also try to associate with REB Research).

I’ve updated the cup to add more elements: I think it’s great. You can buy it for $45 through our web-site, or for $40 by e-mailing me (reb@rebresearch.com). Or if you do something really cool, I may send you one for free.

REB Research, Periodic table coffee cup

REB Research, Periodic table coffee cup

By the way, I only use 4 digits for the atomic weight; I can think of no application where a normal person needs more.

How hydrogen and/or water can improve automobile mileage (mpg)

8 Replies

In case you’ve ever wondered why it was that performance cars got such poor milage, or why you got such bad milage in the city, the biggest single problem has to do with the vacuum drawn by the engine, some of the problem has to do with the speed of combustion, some has to do with rolling friction, and some with start/stop loss too. Only a very small fraction of the energy is lost on air friction until you reach highway speeds.

Lets consider vacuum loss first as it is likely the worst offender. A typical US car, e.g. a Chevy Malibu, has a 3.5 liter engine (a performance car has an engine that’s much larger). As you toodle down a street at 35 mph, your engine is going at about 2000 rpm, or 33 rps. Since the power required to move the car is far less than the 200 hp that the car could deliver, the air intake is throttled so that the engine is sucking a vacuum of about 75 kpa (10 psi for those using English units). To calculate the power loss this entails, multiply 33*3.5*80; this is about 8662 Watts, or 12 hp. To find the energy use per mile, divide by your average speed, 25 mph (it would be 35 mph, but you sometimes stop for lights). 8 kW/25 mph = .21 kW-hr/mile. One finds, as I’ll show that the car expends more energy sucking this vacuum than pushing the car itself. This is where the majority of the city mpg goes in a normal car, but it’s worse in a high performance car is worse since the engine is bigger. In city driving, the performance mpg will be lower than for a Malibu even if the performance car is lighter, if it has better aerodynamics (it does), and if you never stop at lights.

The two other big places were city mileage goes is overcoming rolling friction and the need to stop and go at lights, stop signs, etc. The energy used for rolling friction is the force it would take to push your car on level ground when in neutral times the distance. For a typical car, the push force is about 70 lbs or 32 kgs or 315 Nt; it’s roughly proportional to the car’s weight. At 35 mph, or 15.5 m/s, the amount of power this absorbs is calculated as the product of force and speed: 15.5*315 = 4882 W, or about 6.5 hp. The energy use is 4.9 kW/35 mph =.14 kWhr/mile. The energy loss from stop lights is similar to this, about .16 kWhr/mile, something you can tell by getting the car up to speed and seeing how far it goes before it stops. It’ll go about 2-3 blocks, a little less distance than you are likely to go without having to stop. Air resistance adds a very small amount at these speeds, about 2000 W, 2.7 hp, or .05 kWhr/mile; it’s far more relevant at 65 mph, but still isn’t that large.

If you add all this together, you find the average car uses about .56 kWhr/mile. For an average density gasoline of 5.6 lb/gal, and average energy-dense gasoline, 18,000 BTU/lb, and an average car engine efficiency of 11000 BTU/kWhr, you can now predict an average city gas mileage of 16.9 mpg, about what you find experimentally. Applying the same methods to highway traffic at 65 mph, you predict .38 kWhr/mile, or 25 mpg. Your rpms are the same on the highway as in the city, but the throttle is open so you get more power and loose less to vacuum.

Now, how do you increase a car’s mpg. If you’re a Detroit automaker you could reduce the weight of the car, or you the customer can clean the junk out of your trunk. Every 35 lbs or so increases the rolling friction by about 1%. These is another way to reduce rolling friction and that’s to get low resistance tires, or keep the tires you’ve got full of air. Still, what you’d really like to do is reduce the loss to vacuum energy, since vacuum loss is a bigger drain on mpg.

The first, simple way to reduce vacuum energy loss is to run lean: that is, to add more air than necessary for combustion. Sorry to say, that’s illegal now, but in the olden days before pollution control you could boost your mpg by adjusting your carburator to add about 10% excess of air. This reduced your passing power and the air pollution folks made it illegal (and difficult) after they noticed that it excess air increased NOx emissions. The oxygen sensor on most cars keeps you from playing with the carburator these days.

Another approach is to use a much smaller engine. The Japanese and Koreans used to do this, and they got good milage as a result. The problem here is that you now had to have a very light car or you’d get very low power and low acceleration — and no American likes that. A recent approach to make up for some of the loss of acceleration is by adding a battery and an electric motor; you’re now making a hybrid car. But the batteries add significant cost, weight and complexity to these cars, and not everyone feels this is worth it. So now on to my main topic: adding steam or hydrogen.

There is plenty of excess heat on the car manifold. A simile use of this heat is to warm some water to the point where the vapor pressure is, for example, 50 kPa. The pressure from this water adds to the power of your engine by allowing a reduction in the vacuum to 50 kPa or less. This cuts the vacuum loss at low speeds. At high speed and power the car automatically increases the air pressure and the water stops evaporating, so there is no loss of power. I’m currently testing this modification on my own automobile partly for the fun of it, and partly as a preface to my next step: using the car engine heat to run the reaction CH3OH + H2O –> CO2 + H2. I’ll talk more about our efforts adding hydrogen elsewhere, but thought you might be interested in these fundamentals.

http://www.rebresearch.com

How and why membrane reactors work

9 Replies

What follows is a shorter, easier version of my old essay on how membrane reactors work to get you past the normal limits of thermodynamics. Also, I’m happy to say, our membrane reactors designs have gotten simpler, and that deserves an update.

At left, is our current, high pressure membrane reactor design, available in one-tube to  72 tube reactor assembly; high pressure, or larger, I suppose. Typically, the area around the shell is used for heat transfer. One needs to add heat to promote endothermic reactions like methanol reforming CH3OH + H2O –> 3H2 + CO2, or ammonia cracking 2NH3 –> N2 + 3H2. You need to take away heat from exothermic reactions, like the water gas shift reaction, CO + H2O –> CO2 + H2. Generally you want to have some heat transfer to help drive the reaction.

The reactor is a shell containing metallic tubes that filter gas. Normally the idea is for hydrogen to be formed in the shell area, and leave by diffusion through the tube walls and down the tubes, leaving as pure hydrogen (only hydrogen can go through metals). We typically suggest to have the reactor sit this way, with the tubes pointed up, and the body half-filled or more with catalyst. According to normal thermodynamics, the extent of a reaction like ammonia cracking will be negatively affected by overall pressure, and the extent of the WGS reaction is only affected by operating temperature. The membrane reactor allows you to remove hydrogen while the reaction progresses, and allows you to get good conversion at higher pressures too. That’s because hydrogen removal shifts the equilibrium so the reaction goes further. The effect is particularly significant at higher pressures. By combining the steps of reaction with separation, we can operate a higher pressures, delivering ultra high purity, avoiding the normal limitations of thermodynamics.

The water-gas reaction, CO + H2O –> CO2 + H2, deserves special mention since it’s common and exothermic. In a normal reactor, your only option to drive the reaction to near completion is by operating at low temperature where the catalyst barely works, 200 °C, or lower. You also have to remove the heat of reaction. In a membrane reactor, you can operate at a much higher temperature, especially if you work at higher pressure. At higher temperature the catalysts work better, and you don’t have to work so hard to remove heat.

At our company, REB Research, we sell membrane reactors; and catalysts, membrane tubes, and consulting.