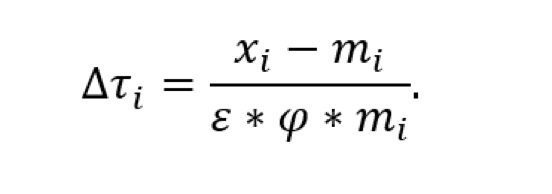We have a trade imbalance with many countries, it causes a loss of American jobs, and a transfer of currency abroad. This imbalance is not all negative, of course, it provides US consumers with cheaper consumer goods. Trump would like to eliminate the imbalance using tariffs. He hopes that this will create jobs, and that the money raised will help balance the US budget. He’s already moved to end income taxes on tips expecting to replace that tax with tariff income. Trump claims that the tariffs are not inflationary compared to current the tax system that he claims has been hacked by the elites. In past essays, I’ve discussed the pluses and minuses of tariffs here, and here. Now I’d now like to derive the formula Trump uses, see below. The proposed tariff for any country or region, i, he calls ∆τi.
In the equation at left, χi = our exports to country, i. Similarly, mi = our imports from that country. The difference between these two is our trade imbalance, something he’d like to set to zero. There are two other greek terms that I will discuss, ε and φ. These are the elasticity of elasticity of consumption to price, and the elasticity of price to tariffs. Trump uses an asterix here to indicate multiplication. I will use a, more normal, “dot” symbol, •, to the same purpose. For most countries, he takes the two elasticities to cancel to 2, and produces a chart.
Let’s say that the dollar amount we currently buy from some country, i, = mi = ni • Pi, where ni is the number of items bought from this country, and Pi is the average price. The intended effect of tariffs is to reduce mi by raising Pi, the price consumers pay for goods from that country. This increase is certainly inflationary in terms of the consumer: a consumer of French wine will pay more per bottle unless he/she switches to US wine. Typically this price rise is not inflationary in terms of the country as a whole, because the producer likely swallows some of the tariff, so for the country as a whole, we pay less per bottle of French wine. The customer does not see that, but it’s worth noting. Trump sees things this way.
Back to the formula, we need to figure out how much the price will go up and how much sales will change. Economists have elasticity numbers for both these relations, denoted φ and ε. We can say that, for any country, I, the rise in the price of the average product is ∆Pi = Pi•∆τi •φ. Where Pi is the original price, ∆τi is the tariff, and φ is the fraction of this tariff that gets passed on to the consumer. A typical value is φ= 1/2 though some claim less. Assuming φ= 1/2 , if we add a 20%=∆τi tariff, as on on French wine, the consumer price will rise by 10%, a change that will cause him/her to buy less.
How much less will the consumer buy? That’s determined by the elasticity of sales, ε. This is the fractional decrease in the number items bought per fractional rise in the price. In math terms, ∆ni /ni = -ε∆Pi/Pi where ε is the elasticity. Now, since ∆Pi = Pi•∆τi •φ, we find that:
∆ni = -ni•ε•∆τi •φ.
There is evidence to suggest that, for the average product, ε equals about 2, and also evidence that it’s 4. Trump prefers 4, and uses it for his calculations. I prefer 2, and will get nearly the same tariffs at the end. Whatever our preferred value for ε, our next step is to use the following approximation, accurate for small ∆(mi);
∆mi = ∆(ni•Pi) = ∆ni•Pi, + ni•∆Pi .
Trump seems to ignore the second term. Perhaps because it can either be positive or negative, as I’d mentioned above, depending on whether you look at things in terms of the customer or of the US as a whole. I’ll keep it in, writing this term in lighter text. In the end I will calculate a fairly similar tariff to Trump:
∆mi = -ni•ε•∆τi •φ•Pi + ni•Pi•∆τi •φ.
Rearranging the above, and recalling that ni•Pi• =mi, you can find the appropriate tariff to eliminate the trade imbalance.
∆τi = -∆mi /(ε • φ• mi + φ•mi) .
To make the trade imbalance go away, you need -∆mi = χi-mi . Thus,
∆τi = χi-mi /(ε • φ • mi + φ•mi)
This is the Trump formula with an extra term in light text. If you ignore that term and use the values Trump prefers, ε =4 and φ=1/2, you get the exact values of the tariffs he listed on the chart for most countries — those with positive trade imbalances.
∆τi = χi-mi / 2 mi
Now, I’d like to put back in the missing term, and use the (better) values, values I would trust, ε =2 and φ=1/2. Using those values, I find the tariff should be slightly higher.
∆τi = χi-mi / 3/2 mi .
I should note that some countries are creating to these trips by raising their own tariffs, and some are lowering theirs. This will cause a change in the imbalance of trade, and Trump will have to change the tariff schedule periodically to keep up.
Robert Buxbaum, April 10, 2025.